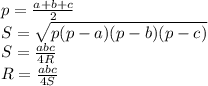

Sabcd = 30 кв. ед.
Объяснение:
Проведем СЕ ║ BD, тогда BCED - параллелограмм, так его противоположные стороны параллельны. Значит,
СЕ = BD = 5
DE = BC = 3
Пусть СН - высота трапеции, тогда СН - и высота треугольника АСЕ.
Площадь трапеции:
Sabcd = 1/2 · (AD + BC) · CH
Площадь треугольника АСЕ:
Sace = 1/2 · AE · CH = 1/2 · (AD + DE) · CH = 1/2 (AD + BC) · CH = Sabcd
Итак, можно найти площадь треугольника АСЕ (в нем известны все три стороны). А площадь трапеции равна площади этого треугольника.
По теореме, обратной теореме Пифагора, проверим, не является ли этот треугольник прямоугольным:
AE² = AC² + CE²
13² = 12² + 5²
169 = 144 + 25
169 = 169 - равенство верно, треугольник прямоугольный.
Sace = 1/2 · AC · CE = 1/2 · 12 · 5 = 30
Sabcd = 30 кв. ед.
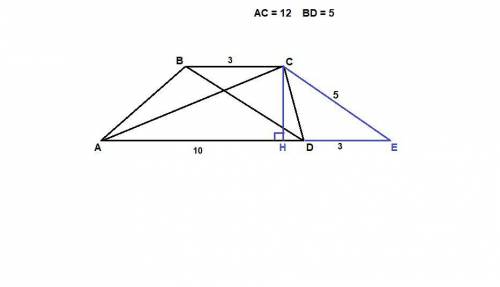
Так, ∠AOB = 2α,
∠BOC = 2β,
∠COD = 2γ.
Значит по условию у нас 2α + 2γ = 180°.
Пусть K и M – точки на биссектрисах углов AOC и BOD соответственно.
Тогда ∠KOC = α + β, ∠BOM = β + γ.
Следовательно, ∠KOM = ∠KOC + ∠BOM – ∠BOC = (α + β) + (β + γ) – 2β = α + γ = 90°