Question

(с чертежами) . 1. прямые а и b пересекаются. прямая с является скрещивающейся с прямой а. могут ли прямые b и с быть параллельными? 2. плоскость проходит через середины боковых стороны ав и сd трапеции abcd – точки m и n. а) докажите, что аd параллельна альфа. б) найдите вс, если ad = 10см, mn = 8см. 3. прямая ма проходит через вершину квадрата abcd и не лежит в плоскости квадрата. а) докажите, что ма и вс – скрещивающиеся прямые. б) найдите угол между прямыми ма и вс, если mad = 45.

Answer 1

1. Могут.

2. б) 6 см

3. б) 45°

Объяснение:

1. Пересекающиеся прямые а и b задают плоскость α. Прямые а и с скрещивающиеся, значит прямая с не лежит в плоскости α.

Прямые с и b могут быть параллельными.

2.

а) Так как точки М и  N принадлежат плоскости трапеции и плоскости α, то MN - линия пересечения плоскостей.

MN - средняя линия трапеции, значит

AD║MN, ⇒  AD║α (если прямая параллельна некоторой прямой, лежащей в плоскости, то она параллельна плоскости).

б)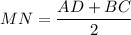 $MN=\dfrac{AD+BC}{2}$

AD + BC = 2MN

BC = 2MN - AD = 2 · 8 - 10 = 16 - 10 = 6 см

3. Признак скрещивающихся прямых: если одна прямая лежит в плоскости, а другая пересекает эту плоскость в точке, не лежащей на первой прямой, то прямые скрещивающиеся.

а) ВС лежит в плоскости (АВС),

МА пересекает (АВС) в точке А,

А не лежит на прямой ВС, значит

МА и ВС скрещивающиеся.

б) ∠(МА, AD) = 45° по условию,

BC║AD, значит

∠(МА, ВС) = 45°