№1
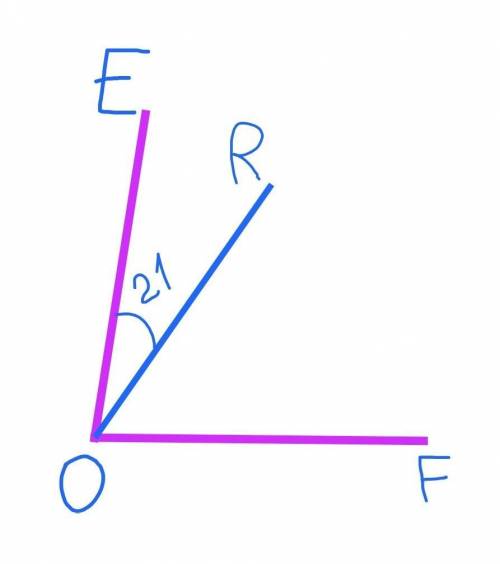
Угол ЕОR=21° по условию
Угол ROF в 3 раза больше угла ЕОR, тогда угол ROF=21°*3=63°.
Угол ЕОF=угол EOR+угол ROF=21°+63°=84°
ответ: 84°
№2
Пусть длина ВС – х, тогда длина АС – 2х
АВ=АС+ВС;
15=2х+х
15=3х
х=5
Тогда длина ВС=5 см, а длина АС=2*5=10 см.
ответ: 10 см, 5 см
№3
а) Угол смежный углу КОЕ – это угол СОЕ (прямая СК и общая сторона ОЕ) или угол NOK (прямая NE и общая сторона ОК)
ответ: два варианта. Выбирай любой.
b) 1 пара: угол КОЕ и угол CON (пересекающиеся прямые СК и NE)
2 пара: угол СОЕ и угол KON (пересекающиеся прямые СК и NE)
c) Так как углы КОЕ и CON вертикальны, то они равны. Угол CON=46° по условию, тогда и угол КОЕ=46°.
d) Угол СОК – развернутый, тоесть он равен 180°;
Угол РОК=65° по условию;
Угол CON=46° по условию;
Угол PON=угол СОК–угол РОК–угол CON=180°–65°–46°=69°
ответ: 69°
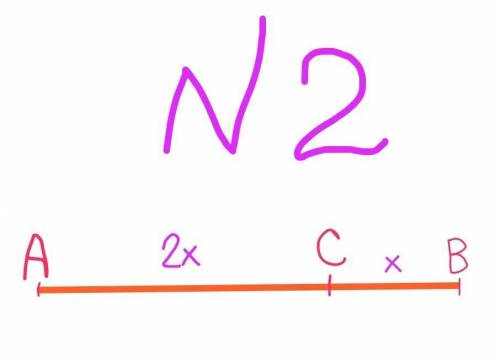
1. Обазанчим пар-мм: ABCD, начиная с нижнего левого угла, точка М - точка пересечения биссектрис, M лежит на АВ
2. Углы ВСМ и МСD равны, т.к. СМ - биссектриса угла С, углы ADM и MDC равны, т.к. DM - биссектриса угла D
3. Приме за меньшую сторону ВС=AD=26 (т.к. противолежащие стороны в пар-мме равны и параллельны)
4. угол MCD=углу CMB как накрест лежащие, при пересечении параллельных прямых CD и АВ секущей МС ⇒ ΔМВС - равнобедренный, ВС=ВМ=26
5. угол МDC=углу DMA как накрест лежащие, при пересчении прямых параллельных CD и AB секущей MD ⇒ ΔMAD - раавнобедренный, AD=AM=26
6. АВ=CD - большая сторона, AB=BM+AM=26+26=52
ответ: большая сторона = 52
Замечательные точки треугольника — точки, местоположение которых однозначно определяется треугольником и не зависит от того, в каком порядке берутся стороны и вершины треугольника.
Обычно они расположены внутри треугольника, но и это не обязательно. В частности, точка пересечения высот может находиться вне треугольника.
пересечение бисектрис, медиан, серидинных перпендикуляров, и высотна самом деле их не четыре. вот все
Точки пересечения:
Медиан — центроид, центр тяжести;
Биссектрис — инцентр, центр вписанной окружности;
Высот — ортоцентр;
Серединных перпендикуляров — центр описанной окружности;
Cимедиан — точка Лемуана;
Перпендикуляров, восстановленных из вершин правильного, вписанного в исходный треугольник, — точка Аполония;
Биссектрис серединого треугольника (его инцентра) — точка Шпикера;
Точки пересечения отрезков, соединяющих вершины треугольника:
c точками касания противоположных сторон и вписанной окружности — точка Жергона;
c точками касания противоположных сторон и вневписанной окружности — точка Нагеля;
c соответствующими свободными вершинами равносторонних треугольников, построенных на сторонах треугольника — точка Ферма, если в треугольнике ни один из углов не превосходит 120°, то точка Торричелли существует и совпадает с точкой Ферма;
c соответствующими свободными вершинами треугольников, подобных исходному треугольнику и построенных на его сторонах — точки Брокара;
Центр окружности девяти точек.