после построения mn получается треугольник mne, подобный треугольнику cde по первому признаку подобия (угол е - общий, углы с и nme равны как соответственные углы при пересечении двух параллельных прямых cd и mn секущей се). поскольку треугольники подобны, то
< mne = < cde = 68°
зная, что развернутый угол равен 180°, находим угол dnm:
< dnm = 180 - < mne = 180 - 68 = 112°
поскольку dm - биссектриса, то угол mdn = < cde : 2 = 68 : 2 = 34°
зная два угла треугольника dmn, находим неизвестный угол:
< dmn = 180 - < mdn - < dnm = 180 - 34 - 112 = 34°
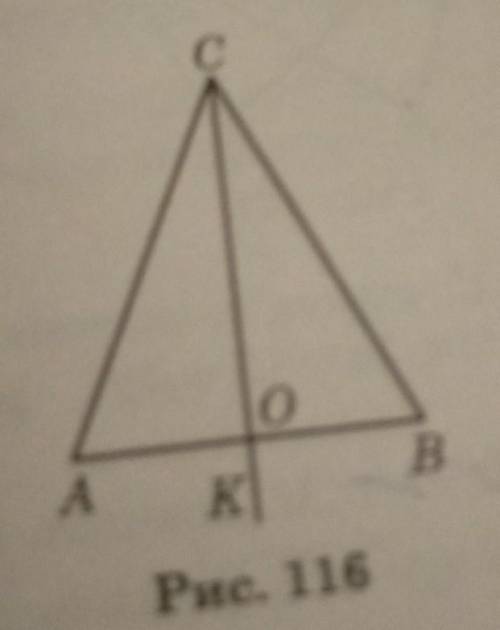
Треугольник ΔCOA = ΔCOB по второму признаку равенства треугольников так как по условию AB ⊥ CK, а так как точка O принадлежит прямой CK, то AB ⊥ CO ⇒ ∠COA = ∠ COB = 90°;Так как CO - биссектриса ∠ACB по условию, то угол ∠ACO = ∠BCO , а сторона CO - общая. Так как треугольник ΔCOA = ΔCOB, то соответствующие элементы треугольников равны, тогда BO = OC.