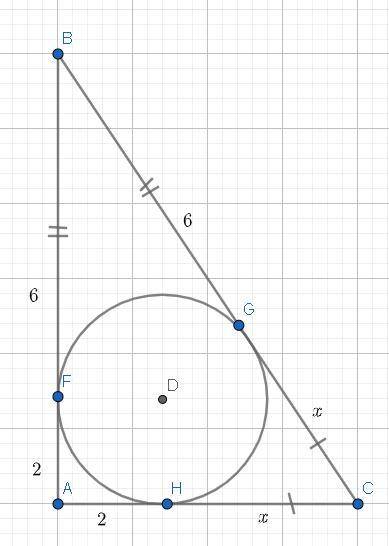
В случае окружности, вписанного в прямоугольный треугольник — точки касания делят все стороны на некие равные отрезки.
То есть: Через точку B — проведены 2 касательные: катет BA & гипотенуза BC.
В точках касания — отрезки друг другу равны(теорема о 2 касательных, проведённых с одной точки), тоесть: BF == BG.
BF == BG ⇒ BF == BG = 6.
Одни и те же действия с отрезками FA & AH, они тоже друг другу равны, так как их касательные проведены с одной точки.
FA == AH = 2.
Точно так же с отрезками HC & GC: HC == GC = x.
По теореме Пифагора:
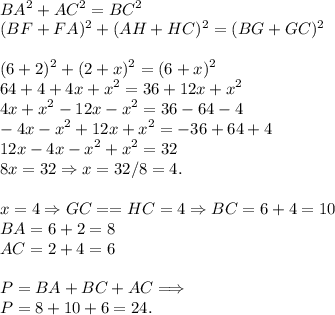
Вывод: P = 24 см.
См. Объяснение
Объяснение:
Если расстояние от центра окружности до прямой больше радиуса окружности,... то эти прямая и окружность не имеют общих точек.
ответ: 1-4
Отрезки касательных, проведенных к окружности из одной точки,...расположенной вне этой окружности, равны.
ответ: 2-1
Если расстояние между центрами двух окружностей равно сумме или разности их радиусов,.. то эти окружности касаются.
ответ: 3-2
Если расстояние между центрами двух окружностей меньше суммы радиусов и больше их разностей, то эти окружности пересекаются.
ответ: 4-3
57°, 93°, 30°.
Объяснение:
1) По определению внешний и внутренний углы треугольника при одной вершине являются смежными, тогда их сумма равна 180°, Угол, смежный с внешним углом в 87°, равен 180° - 87° = 93°.
2) Найдём третий угол треугольника.
По теореме внешний угол треугольника равен сумме двух внутренних, не смежных с ним, тогда
87° = 57° + х
х= 87° - 57° = 30°.
ответ: внутренние углы треугольника равны 57°, 93°, 30°.