треугольник abc - прямоуголный, уголС=90, АВ=2АС=2*15=30 см (по св-ву катета лежащего против угла в 30)... из т.п. ВС^2 = AB^2 - AC^2 = 30^2 - 15^2 = 900 - 225 = 675, BC=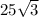
Периметр равен P=2*(a+b)
12) P1 = 2*(6+4)=20 P2 = 2*(11.5+7)=37
13) Пусть а=12,4, следовательно b1 = 12.4 - 0.8 = 11.6, b2 = 12.4 + 1.6 = 14, b3 = 12.4 / 4 = 3.1. Тогда P1 = 2*(12.4+11.6) = 48? P2 = 2*(12.4 + 14) = 52.8, P3= 2*(12.4+3.1)=31
14) Так как P=2*(a+b), следовательно a+b = P/2. Тогда 3 + b = 9.2 и b = 9.2-3=6.2. 7 + b = 9.2, тогда b = 9.2 - 7 = 2.2
15) P=24 a1=x, b1 = x+4, следовательно 24 = 2*(x+x+4), 12 = 2x +4, 2x=8, x=4. Тогда a = 4, b = 8. P=24 a1=x, b1 = x-6, следовательно 24 = 2*(x+x-6), 12 = 2x -6, 2x=18, x=9. Тогда a = 9, b = 3. P=24 a1=x, b1 = 2x, следовательно 24 = 2*(x+2x), 12 = 3x, x=4. Тогда a = 4, b = 8.
16) a+b = 12 и a:b = 1:2, следовательно a=x b =2x, тогда x+2x=12, x=4 и a=4 b = 8
a+b = 12 и a:b = 3:2, следовательно a=3x b =2x, тогда 3x+2x=12, x=2.4 и a=7.2 b = 4.8
17)в параллелограмме противоположные углы равны,а односторонние в сумме дают 180 градусов. Следовательно в параллелограмме два угла по 42 градуса и 2 угла по 180-42 = 138 градусов.
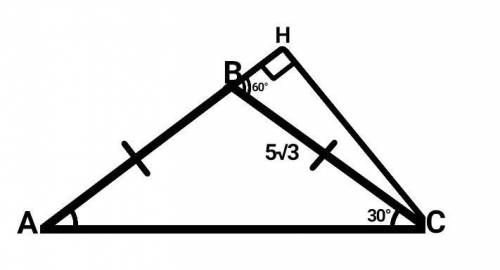
Дано :
∆АВС — равнобедренный (АС — основание).
АВ = ВС = 5√3.
<С = 30°.
СН — высота.
Найти :
СН = ?
В равнобедренном треугольнике углы при основании равны.Следовательно —
<А = <С = 30°.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.То есть —
Внешний <В = <А + <С
Внешний <В = 30° + 30°
Внешний <В = 60°.
Рассмотрим прямоугольный ∆ВСН (СН лежит вне треугольника, так как ∆АВС — тупоугольный).
BC — гипотенуза (так как лежит против угла в 90°).
Тогда —
Sin(<HBC) = CH/BC (по определению синуса острого угла прямоугольного треугольника)
Sin(60°) = CH/(5√3)
Обозначим СН за х.
Тогда —
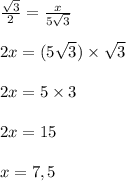
СН = 7,5 (ед).
7,5 (ед).
— — —
Надеюсь, я Вам. Есть вопросы по поводу решения? Задавайте в комментариях.
получается прямоугольный треугольник, т.к 180-30-60=90 градусов угол С, катет АС= 2/1 АВ, получается 15*2=30, а если дальше находить сторону ВС то по теореме пифагора