В равнобедренный треугольник АВС , АВ=ВС=15 , АС=24, вписана окружность (О; r). Найдите r.
Объяснение:
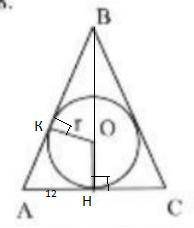
1)Пусть ВН ⊥АС. Центр вписанной окружности О лежит в точке пересечения биссектрис. В равнобедренном треугольнике биссектриса совпадает с высотой ⇒поэтому О лежит на высоте ВН.
АН=42 :2=12( т.к. ВН и медиана ) . Будем искать r из ΔКВО.
2) ΔАВН-прямоугольный, по т. Пифагора ВН=√(15²-12²)=9. Тогда отрезок ВО можно выразить так ВО=9-r.
По свойству отрезков касательных АН=АК=12⇒КВ=15-12=3.
3) ΔКВО-прямоугольный , по свойству радиуса , проведенного в точку касания . По т. Пифагора ВО²=ОК²+КВ²
(9-r)²=r²+3² ,81-18r+r²=r²+9 ,18r=72 , r=4 .
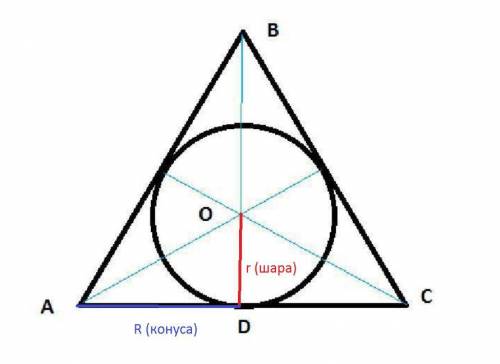
Осевое сечение конуса – равнобедренный треугольник АВС.
АВ=ВС – образующие.
BD– высота конуса, а также высота, медиана и биссектриса равнобедренного треугольника.
О–центр вписанной в треугольник АВС окружности и центр вписанного в конус шара.
ОD=r .
AD=R .
Из прямоугольного треугольника
tg∠OAD = tg(α/2) = r/R . Отсюда r = Rtg(α/2).
ОА– биссектриса угла ВAD, так как центр вписанной в треугольник окружности– точка пересечения биссектрис.
Высота конуса H = R/tg(α/2).
V(шара) = (4/3)πr³ = (4/3)πR³tg³(α/2).
V(конуса)=(1/3)S(осн)·H=(1/3)·πR²·R/tg(α/2) = (1/3)·πR³/tg(α/2).
Разделим V(конуса) на V(шара).
V(конуса) / V(шара) = ( (1/3)·πR³/tg(α/2)) / ((4/3)πR³tg³(α/2)) = 4tg³(α/2)tgα.
ответ: V(конуса) = V(шара) / (4tg³(α/2)tgα).
Проведем высоту из вершины меньшего основания к большему. Получим прямоугольный треугольник, один из углов которого 60 градусов. Тогда другой угол будет 180-90-60=30 градусов. Сторона, лежащая напротив угла в 30 градусов (отрезок большего основания) равна половине гипотенузы, т.е. 5 см. Тогда, т. к. трапеция равнобедренная, длина меньшего основания равна 16-(2*5)=6 см.
ответ: 6 см.