
60°,60°,60°.
Объяснение:
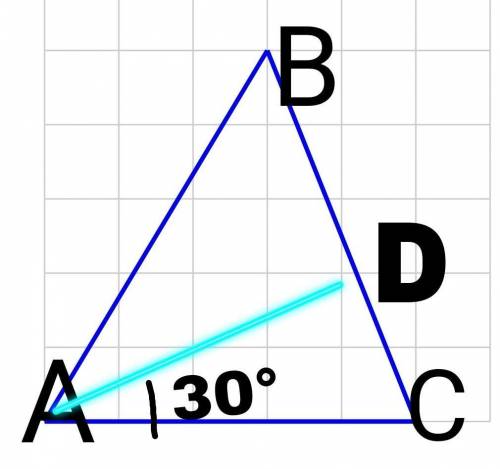
Так как в равнобедренном треугольнике высота является и биссектрисой, то АD - биссектриса, значит угол А = 30°+30°=60°. Так как АD - высота, то угол АDC=90°, следовательно, треугольник АDC-прямоугольный. Угол С=90°-30°=60°(сумма острых углов прямоугольного треугольника = 90°).
Угол В=180°-60°-60°=60°(сумма углов треугольника = 180°).
Либо же есть 2 вариант (попроще).
Находишь угол А=60°(по решению сверху), пишешь, что в равнобедренном треугольнике углы при основании равны, значит, угол А=углу С. А дальше находишь угол В, отнимая от 180° 120°, и получаешь 60°.
168°.
Объяснение:
Докажем теорему о сумме внутренних углов выпуклого шестиугольника.
Построим произвольный выпуклый шестиугольник АВСDEF, и из вершины А проведём диагонали:
АС - она отсечёт треугольник АВС;
АD - получим ещё один треугольник - АСD;
АЕ - получим ещё 2 треугольника: ADE и АFE.
Проведя диагонали, мы представили 6 внутренних углов выпуклого шестиугольника в виде суммы внутренних углов 4-х треугольников, которая равна: 180° · 4 = 720°, где
180° - сумма внутренних углов одного треугольника.
Таким образом, мы доказали, что сумма внутренних углов любого выпуклого шестиугольника равна 720°.
Это значит, что если в шестиугольнике 3 угла равны 72° каждый, а 3 других угла равны между собой, то градусные меры трёх других углов равны:
[720 - (72 · 3)] : 3 = (720 - 216) : 3 = 504 : 3 = 168°.
ответ: 168°.
2м
Объяснение:
Пусть из точки М опустили перпендикуляр на площадь прямоугольника ABCD через точку А. Тогда по условию, MB=5м, MC=11м, MD=10м. Найти MA.
По теореме о 3х перпендикулярах: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость. Значит поскольку BC⊥AB, то BC⊥MB. По т-ме Пифагора BC²=MC²-MB²=121-25=96.
MA⊥AD по условию, значит по т-ме Пифагора MA²=MD²-AD². AD=BC => MA²=100-96=4
MA=2