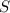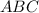
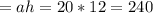△
см².
Пошаговое решение:
Дано:
△;
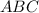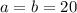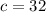см;
см;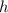
- высота;
Найти: △;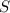
Решение:
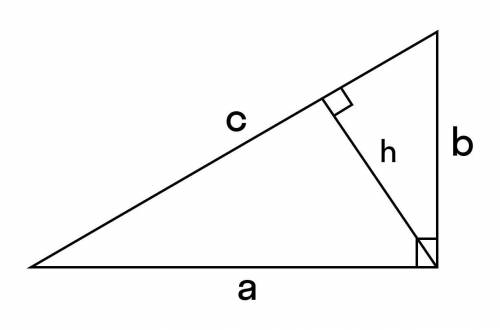
Высота в равнобедренном треугольнике является одновременно и медианой, и биссектрисой. Медиана, проведённая из вершины угла в противоположную сторону, делит её на две равные части. Соответственно, проведённая из противоположного основанию угла высота делит его пополам. Перпендикуляр образует два прямоугольных треугольника. Боковая сторона 
равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
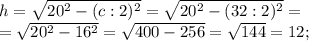
Находим площадь, умножив основание на высоту и поделив на 2.△
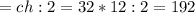(см²)
|AC| = 10 см.
Объяснение:
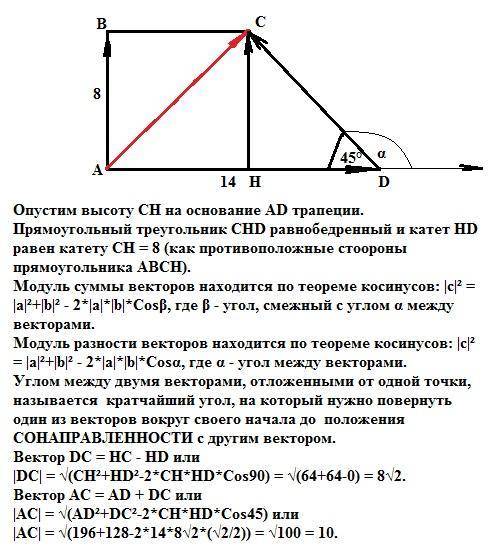
Опустим высоту СН на основание AD трапеции.
Прямоугольный треугольник СНD равнобедренный и катет HD равен катету СН = 8 (как противоположные стоороны прямоугольника АВСН).
Модуль суммы векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosβ, где β - угол, смежный с углом α между векторами.
Модуль разности векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosα, где α - угол между векторами.
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения СОНАПРАВЛЕННОСТИ с другим вектором. Итак,
Вектор DC = НС - HD или
|DC| = √(CH²+HD²-2*CH*HD*Cos90) = √(64+64-0) = 8√2.
Вектор АС = AD + DC или
|AC| = √(AD²+DC²-2*CH*HD*Cos45) или
|AC| = √(196+128-2*14*8√2*(√2/2)) = √100 = 10.
ответ: Длина вектора (модуль) АС = 10 см.
Для начла надо найти катет ВС:
ВС^2=169-25=144
ВС=12
Теперь рассморим треугольник SCB.Аналогично, находим гипотенузу ЕВ, которая будет являться искомым расстоянием (по теореме о трех перепендикулярах):
ЕВ^2=256+144=400
ЕВ=20