
1) пусть стороны АВ=5, ВС=8 и АС=12 и стороны А1В1=15, В1С1=24 и А1С1=26, относятся как A1B1/AB=15/5=3 и т.д.
значит по третьему признаку подобия треугольники подобны
Свойства подобных треугольников Отношение площадей подобных треугольников равно квадрату коэффициента подобия
S1/S=3^2=9
2) Если угол при вершине равнобедренного треугольника равен 38°, то углы при основании будут равны = 71°. Значит два угла при основании одного треугольника равны двум углам при основании другого треугольника, т.е. они подобны по первому признаку подобия треугольников.
3) 1) AB=AD-BD=22-8=14; По теореме Фалеса AB:AC=BD:CE; AC=AB*CE:BD=14*10:8=17,5. 2) AE=AC+CE=8+10=18; Треугольники ADE и ABC подобны, АЕ:AC=DE:BC; DE=AE*BC:AC=18*4:8=9;
Для решения нам нужно найти высоту
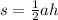
Вот формула площади треугольника. Но так как треугольник прямоугольный, то высота=катет
Здесь используем формулу Пифагора
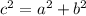
с — гипотенуза, a и b - катеты
Гипотенуза у нас известна, значит используем обратную формулу
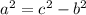
a²=20²-15²=400-225=175
a²=175
Так как в таблице квадратов такого числа нет, значит
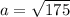
Мы нашли катет, тобишь высоту.
Далее пользуемся формулой площади.
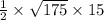
(a — высота, b — основание, по свойствам прямоугольного треугольника)
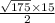
Не думаю, что нужно преобразрвывать, ибо там получится число с большим количеством числел после запятой, если конкретно, то:
99,215674164922147143810590761472265964134
Так что, думаю, лучше оставить формулой (где с дробью)
Можно также ещё преобразовать корень:
(не могу дополнить с формулой, увы, так что "V" = корень, ' — где он заканчивается)
Разбиваем корень на два множителя, один из которых можно будет вычислить.
V175' =V25' × V7`= 5V7'
Пять корней из семи. Значит в том ответе с дробью в числителе можно написать 5V7×15
Объяснение:
1)Две прямые на плоскости называются параллельными если они не пересекаются. Два отрезка называются параллельными если они лежат на параллельных прямых
2)Прямая с называется секущей по отношению к прямым а и в если она пересекает их в двух точках
3)Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны
4)Если при пересечении двух прямых секущей соответственные углы равны то прямые параллельны
5)Если при пересечении двух прямых секущей сумма односторонних углов равна 180 то прямые параллельны
6)с чертежного угольника и линейки
7)Утверждения которые принимаются в качестве исходных положений на основе которых доказываются теоремы называются аксиомами
Пример:Через любые две точки проходит прямая и притом только одна
8)Через точку не лежащую на данной прямой проходит только одна прямая параллельна данной
9)Через точку не лежащую на данной прямой проходит только одна прямая параллельна данной
10)Утверждение которое выводится непосредственно из аксиом или теорем