Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
ВО:ОК=2:1
SO:ON=2:1
В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки.
В ∆ DOK и ∆ BON равны две стороны и углы между ними при вершине О как вертикальные. Следовательно, эти треугольники равны по первому признаку.
--------
∆ DOK и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины.
А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.
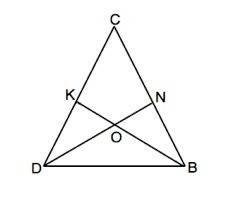
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
ВО:ОК=2:1
SO:ON=2:1
В равностороннем треугольнике медианы равны. Следовательно, равны и их сходственные отрезки.
В ∆ DOK и ∆ BON равны две стороны и углы между ними при вершине О как вертикальные. Следовательно, эти треугольники равны по первому признаку.
--------
∆ DOK и ∆ BON равны и по 3-му признаку, т.к. у равных сторон равны и их половины.
А, поскольку медианы являются здесь и биссектрисами и высотами, то можно доказать их равенство и по второму признаку.

ответ: площадь диагонального сечения пирамиды 14 см².
Диагональ квадрата АС - это диаметр описанной около основания окружности.
АО=R
R = a/√2, где а - сторона квадрата
Диагональное сечение пирамиды - это равнобедренный ΔASC.
Формула площади треугольника: S = 1/2 АС * SO
Высоту SO находим как катет прямоугольного треугольника ΔASO по теореме Пифагора