По формуле середины отрезка 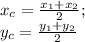
ищем координаты середины отрезков AC и BD
АС: 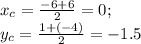
(0;-1.5)
BD: 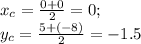
(0;-1.5)
Середины совпадают
По признаку параллелограмма (если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам - то он параллелограмм), делаем вывод, что ABCD - параллеллограмм
По формуле расстояний между двумя точками, задаными координатами
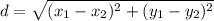
находим длины диагоналей AC и BD
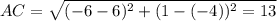
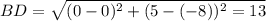
Диагонали равны
По признаку прямоугольника (если диагонали параллелограмма равны - то он парямоугольник), делаем вывод, что ABCD - прямоугольник.
Доказано
OB = OC = 9 см
AB = 12 см
Отрезки касательных к окружности, проведенные из одной точки равны
AB = AC (AO - общая сторона, угол ABO = угол ACO = 90, BO = OC)
AC = 12 см
AO - гипотенуза
AO = 15 cм