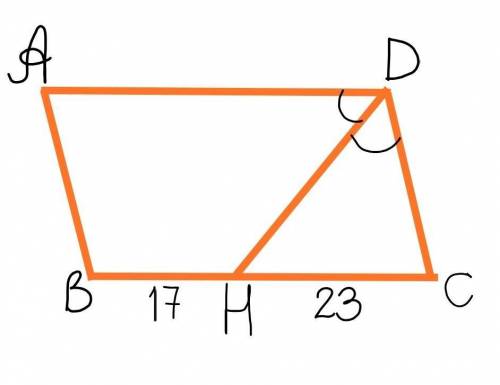
Так как противоположные стороны параллелограмма параллельны, то угол СНD=угол ADH как накрест-лежащие при параллельных прямых AD u BC и секущей DH.
Биссектриса делит угол на два равных угла.
Следовательно угол СDH=угол ADH.
Исходя из найденного: Угол СHD=угол CDH.
Тогда ∆CHD – равнобедренный с основанием HD.
У равнобедренного треугольника боковые стороны равны, тоесть CD=CH=23 см
Противоположные стороны параллелограмма попарно равны.
Следовательно: AD=BC=BH+HC=17+23=40 см; AB=CD=23 см.
Периметр параллелограмма – это сумма длин всех его сторон.
Тоесть Р=AD+AB+BC+CD=40+23+40+23=126 см.
ответ: 126 см.
Найдем искомую точку для оси ординат Оу.
Пусть С(0;у) - точка, равноудаленная от точек А и В.
Тогда:
(0 - (-3))^2 + (y - 5)^2 = (0 - 6)^2 + (y - 4)^2,
или, после преобразований, (у - 5)^2 - (у - 4)^2 = 27,
9 - 2y = 27,
y = -9.
Следовательно, координаты искомой точки С(0; -9)
Проделывая то же самое для точки М(х; 0) на оси абсцисс, получим координаты точки М (1; 0).
ответ: (0;-9), (1;0)