2х+2у=30
ху=56
х=(30-2у):2
х=15-у
у(15-у)=56
15у-у(квадрат)=56
-у(квадрат)+15у-56=0
D=225-4(-1)*(-56)=1
х1=(-15+1):(-2)=7
х2+(-15-1):(-2)=8
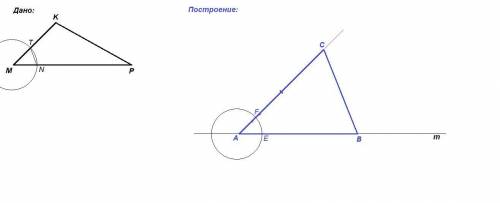
1. На прямой m отложим отрезок АВ = МР.
2. Построим ∠А = ∠М. Для этого:
построим окружность произвольного радиуса с центром в точке М; точки пересечения этой окружности со сторонами угла М обозначим N и Т;
построим окружность с тем же радиусом с центром в точке А; Е - точка пересечения этой окружности с отрезком АВ;проведем дугу с центром в точке Е и радиусом, равным NT; F - точка пересечения дуги с окружностью;проведем луч AF.3. На луче AF дважды последовательно отложим отрезок, равный МК, получим точку С.
4. Соединим точки В и С.
ΔАВС - искомый.
Задача может не иметь решения, если в данном треугольнике сторона МК большая и не выполняется неравенство:
2MK < MP + KP.
P=2a+2b
S=a*b
2a+2b=30
a*b=56
a=56/b
2*56/b+2b=30
b^2-15b+56=0
D=1 b=7 и b=8
a=56/b a=7 и a=8 , что, по сути, одно и тоже.
ответ: 8 и 7