

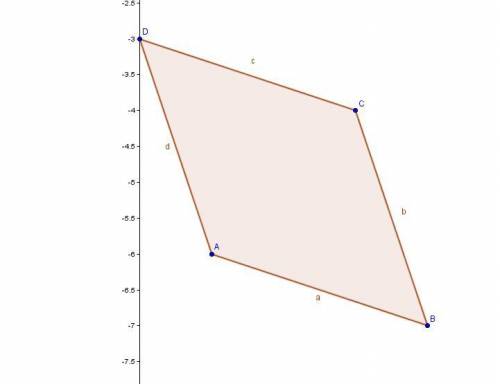
Даны координаты вершин четырехугольника (1;-6), (4;-7), (3;-4), (0;-3).
Проще всего разделить его на 2 треугольника.
Находим длины сторон.
AB (c) = √((xB-xA)² + (yB-yA)²) = √10 = 3,16227766
BC (a) = √((xC-xB)² + (yC-yB)²) = √10 = 3,16227766
AC (b) = √((xC-xA)² + (yC-yA)²) = √8 = 2,828427125
CD = √((xD-xC)² + (yD-yC)²) = √10 = 3,16227766
AD = √((xC-xA)² + (yC-yA)²) = √10 = 3,16227766 .
Площади по Герону.
Периметр Р(АВС) = 9,152982445
Полупериметр р = 4,576491223 .
Площадь S(АВС) = 4,576491223 1,414213562 1,748064098 1,414213562 = √16 = 4
S(ACD) = 4,576491223 1,748064098 1,414213562 1,414213562 = √16 = 4 .
ответ: S(ABCD) = 4 + 4 = 8 кв.ед.
Задание 2. а)Угол КАВ, образованный касательной АК и хордой АВ, проходящей через точку касания А, равен половине величины дуги АВ, заключённой между его сторонами, центральный угол АОВ тоже опирается на дугу АВ, а угол АСВ- вписанный угол, опирающийся на дугу АВ, поэтому равен половине величины центрального угла.
б)Т.о., углы АСВ и КАВ равны. А т.к. АК и КВ - отрезки касательных, проведенных из одной точки к одной окружности, то АК=КВ, т.е. ΔКАВ- равнобедренный.
в) т.к. по условию АС║КВ, то по свойству внутренних накрест лежащих при указанных параллельных прямых и секущей АВ ∠АВК=∠ВАС. значит, по двум углам треугольники КАВ и АСВ подобны, значит, сходственные стороны у них пропорциональны. АВ/ВС=АК/АС=к- коэффициент пропорциональности , Площадь треугольника АВС равна ВС*АС*sin∠ACB; площадь треугольника КАВ равна
АК*АВ*sin∠КАВ. Синусы равных углов равны. Отношение площадей (АК*АВ*sin∠КАВ)/(BC*АС*sin∠ACB)=АК*АВ/ВС*АС=к²; получается, что от угла не зависит отношение. Это для любого треугольника, а если к тому же треугольник АВС равнобедренный с основанием АВ, то все углы в нем по 60°, т.е. он получается равносторонним. т.е. угол и выбирать не надо по этому условию он уже определен. А из того, что угол равен 60°, следует равенство данных треугольников, значит, отношение их площадей равно единице.