Хорда перпендикулярная диаметру, делит его на отрезки5 см и 45см.найдите длину хорды

👇

Увидеть ответ

Ответ:

stockmen

02.07.2022

диаметр=50,радиус,следовательно,равен 25.из центра к хорда проводим радиус,

один катет равен 20,

по теореме пифагора получаем,что половина хорды равна 15,следовательно вся хорда равна 30:)

4,6(3 оценок)

Ответ:

krichilskaatтанюшка

02.07.2022

есть теорема, что если две хорды пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.

Получаем, что произведение отрезков искомой хорды равно 45*5=225 см

Аткже есть свойство, что если диметр перпендикулярен хорде, то он делит ее пополам. Значит эта хорда разделена на равные отрезки, произведение которых равно 225.

ТОгда длина одного отрезка получается √225=15

Тогда длина хорды равна 15*2=30 см.

P.S. если интересно, могу написать почему диаметр перепендикулярный хорде, делит ее пополам.

4,4(28 оценок)

Открыть все ответы

Ответ:

nastasyasidork

02.07.2022

Точка E расположена на расстоянии b от центра O квадрата со стороной a. Найдите расстояние от точки E до вершин квадрата,если отрезок OE перпендикулярен плоскости квадрата.

Решение:
Пусть одна из вершин квадрата обозначается точкой А.
Рассмотрим треугольник ОЕА.
Треугольник ОЕА - прямоугольный так как отрезок ОЕ перпендикулярен плоскости квадрата, а сторона ОА лежит в плоскости квадрата.
Длина катета ОЕ равна b(по условию).
Определим длину ОА как половину диагонали квадрата со стороной а.
Длина диагонали равна а√2.
Следовательно длина другого катета ОА равна (√2/2)*а.
По теореме Пифагора определим длину гипотенузы ЕА
$|EA|= \sqrt{|OE|^2+|OA|^2}= \sqrt{b^2+(( \sqrt{2}/2)a)^2}= \sqrt{b^2+a^2/2}$

ответ: √(b²+0,5a²)

4,4(21 оценок)

Ответ:

German1224

02.07.2022

Замечание: равносторонний треугольник не может быть тупоугольным)))
видимо, опечатка во второй задаче...
Обе задачи очень похожи по логике решения: из двух формул для площади можно установить зависимость между сторонами треугольника или стороной и высотой треугольника и по теореме Пифагора найти нужный отрезок.
1) для любого описанного многоугольника (не только для треугольника) площадь можно вычислить через радиус вписанной окружности:
S = p * r (где p -это полу-периметр)
т.к. треугольник равнобедренный, основание разобьется на два равных отрезка (х) и отрезки касательных, проведенных из одной точки к окружности, равны)))
получим четыре равных отрезка на сторонах треугольника и еще два равных отрезка обозначим (у), осталось записать т.Пифагора...
2) здесь потребуется другая формула для площади вписанного треугольника --через радиус описанной окружности:
S = a*b*c / (4R) и т.к. треугольник тупоугольный (по условию), следовательно, тупой угол треугольника опирается на дугу окружности, которая больше 180°
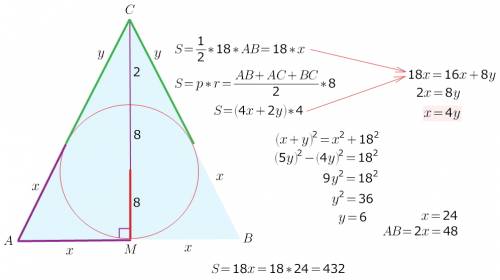
1) высота равнобедренного треугольника, поведённая к основе, равна 18 см, а радиус вписанного круга