
∠DKC = 24°.
Объяснение:
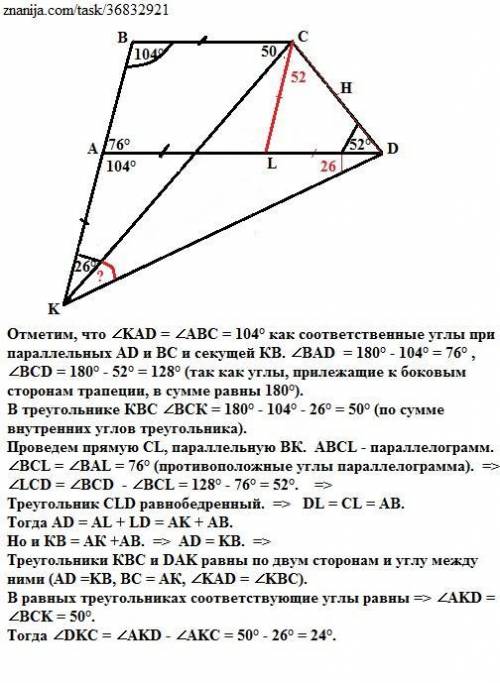
Отметим, что ∠KAD = ∠ABC = 104° как соответственные углы при параллельных AD и ВС и секущей КВ.
∠BAD = 180° - 104° = 76° , ∠BCD = 180° - 52° = 128° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).
В треугольнике КВС ∠ВСК = 180° - 104° - 26° = 50° (по сумме внутренних углов треугольника).
Проведем прямую СL, параллельную ВК.
АВСL - параллелограмм.
∠BCL = ∠BAL = 76° (противоположные углы параллелограмма). =>
∠LСD = ∠BCD - ∠BCL = 128° - 76° = 52°. =>
Треугольник СLD равнобедренный. => DL = CL = AB.
Тогда AD = AL + LD = AK + AB.
Но и КВ = АК +AВ. => AD = KB. =>
Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).
В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 50°.
Тогда ∠DKC = ∠AKD - ∠AKC = 50° - 26° = 24°.
∠DKC = 36°.
Объяснение:
Вот один из вариантов решения:
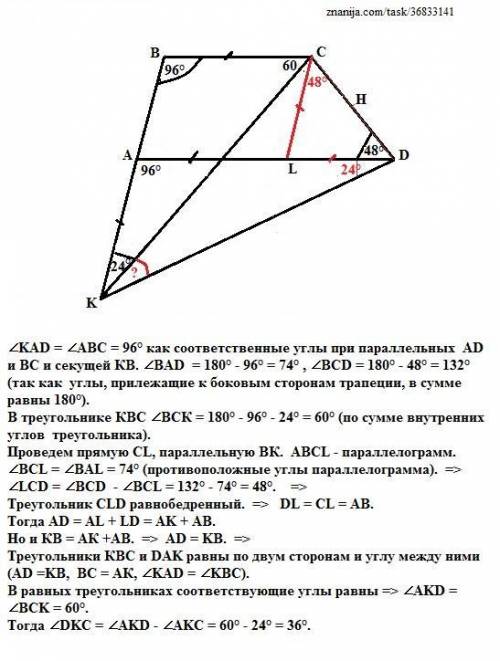
∠KAD = ∠ABC = 96° как соответственные углы при параллельных AD и ВС и секущей КВ. ∠BAD = 180° - 96° = 74° , ∠BCD = 180° - 48° = 132° (так как углы, прилежащие к боковым сторонам трапеции, в сумме равны 180°).
В треугольнике КВС ∠ВСК = 180° - 96° - 24° = 60° (по сумме внутренних углов треугольника).
Проведем прямую СL, параллельную ВК. АВСL - параллелограмм.
∠BCL = ∠BAL = 74° (противоположные углы параллелограмма). =>
∠LСD = ∠BCD - ∠BCL = 132° - 74° = 48°. =>
Треугольник СLD равнобедренный. => DL = CL = AB.
Тогда AD = AL + LD = AK + AB.
Но и КВ = АК +AВ. => AD = KB. =>
Треугольники КВС и DAK равны по двум сторонам и углу между ними (AD =KB, BC = АК, ∠KAD = ∠KBC).
В равных треугольниках соответствующие углы равны => ∠AKD = ∠BCK = 60°.
Тогда ∠DKC = ∠AKD - ∠AKC = 60° - 24° = 36°.
Sпол=200+400√6
V=1000√6
Объяснение:
Дано:
ABCDA1B1C1D1- призма
ABCD- квадрат
A1B1C1D1- квадрат.
АВ=10
<В1DB=60°
1) BD=?
2) B1D=?
3) BB1=?
4) Sбок=?
5) Sпол=?
6) V=?
7) S(BB1D1D)=?
8) S(MKLP)=?
9) S(QGOT)=?
1)
ВD=AB√2=10√2 диагональ квадрата.
2)
cos60°=BD/B1D
1/2=10√2/B1D
B1D=10√2*2=20√2 ед²
3)
∆ВВ1D- прямоугольный
По теореме Пифагора
ВВ1=√(В1D²-BD²)=√((20√2)²-(10√2)²)=
=√(800-200)=√600=10√6 диагональ призмы.
4)
Росн=4АВ=4*10=40 периметр квадрата.
Sбок=Росн*ВВ1=40*10√6=400√6 ед² площадь боковой поверхности призмы.
5)
Sосн=АВ²=10²=100 ед² площадь квадрата.
Sпол=2Sосн+Sбок=200+400√6 ед²
6)
V=Sосн*ВВ1=100*10√6=1000√6 ед³ объем призмы.
7)
S(B1D1DB)=BD*B1B=10√2*10√6=100*2√3=
=200√3 ед² площадь диагонального сечения.
8)
S(PLKM)=BB1*AB=10√6*10=100√6 площадь сечения проходящего через середины противоположных сторон.
9)
QG-средняя линия треугольника ∆А1В1D1
QG=1/2*B1D1=1/2*10√2=5√2
S(QGOT)=QG*BB1=5√2*10√6=50*2√3=
=100√3 eд²