4.а) 50°
х вписанный угол,равен половине центрального, опирающегося на общую дугу.
х=100°/2=50°
5. в) 110°
свойство четырехугольника вписанного в окружность: сумма противолежащих углов =180°
х=180°-70°=110°
6. б) 32°
х вписанный угол, равен половине соответствующего центрального
х= 64°/2=32°
7. в) 60°
угол АВО =90° (свойство касательной к радиусу)
ВА=АС(касательные из одной точки)
треугольники ВАО и ОАС равны по двум сторонам и углу между ними
ВO=DO(радиусы)
ВО=DO=DA
BO=OA/2
OA гипотенуза
свойство угла 30°: катет лежащий против угла 30° равен половине гипотенузы
угол ВАО=30°
угол ВАС=30°×2=60°
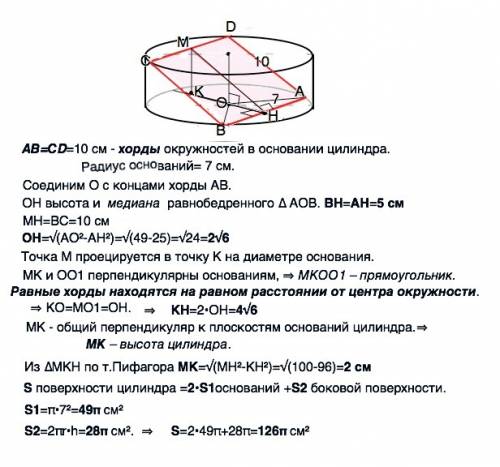
АВСD- квадрат.
О - центр нижнего основания цилиндра, в который вписан квадрат. О1- центр верхнего основания.
АВ=СD=10 см - хорды окружностей в основании цилиндра.
Радиус оснований= 7 см.
Соединим О с концами хорды АВ.
Проведем высоту ОН (она же медиана) в равнобедренном ∆ АОВ. ВН=АН=5 см
МН║ВС=10 см – средняя линия АВСD и пересекает ось цилиндра.
ОН=√(AO²-AH²)=√(49-25)=√24=2√6
Точка М проецируется в точку К на диаметре основания.
МК и ОО1 перпендикулярны основаниям, поэтому МКОО1 – прямоугольник.
Равные хорды находятся на равном расстоянии от центра окружности. ⇒КО=МО1=ОН.
КН=2•ОН=4√6
МК - общий перпендикуляр к плоскостям оснований цилиндра.⇒
МК – высота цилиндра.
Из ∆МКН по т.Пифагора МК=√(МН²-КН²)=√(100-96)=2 см
S поверхности цилиндра =2•S1оснований +S2 боковой поверхности.
S1=π•7²=49π см²
S2=2πr•h=28π см².
S=2•49π+28π=126π см²
1) пусть АВС равнобедренный треугольник
АВ=ВС=15
АС=16
пусть ВК высота
центр описаной и вписаной окпужности О, лежит на высоте ВК
причем ВО-радиус описаной окружности, а ОК- вписаной
АК=1/2*АС=9 см
АВК-прямоугольный треугольник
АВ гипотенуза
из теоремы пифагора,
BK^2=AB^2-AK^2= 225-81=144=12^2
BK=12
, тогда ВО=х
ВО=АО=СО
ОК=12-х
расмотрим треугольник АОК, угол К=90 градусов
АО=х
ОК=12-х
АК=9
из теоремы пифагора
AO^2=AK^2+KO^2
x^2=(12-x)^2+9^2
x^2=144-24x+x^2+81
24x=225
x=225/24
радиус описаной окружности АО=9(9/24)
радиус вписаной окружности ОК=12-9(9/24)=12-225/24=(12*24-225)/24=
=(288-225)/24=63/24=2(15/24)
ответ
радиус описаной окружности 9(9/24)=9.375
радиус вписаной окружности 2(15/24)=2.625