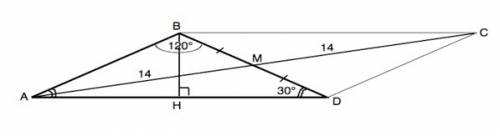
Обозначим данный треугольник АВD.
Примем его боковые стороны равными а.
Проведем высоту ВН.
В равнобедренном треугольнике с углом при вершине 120° углы при основании равны 30°. ⇒
АН=DH=а•cos30°=a√3/2⇒ AD=a√3
Продлим медиану АМ на её длину до т.С.
АС=2 АМ=28.
Соединим В и D с т.С.
ВМ=DM по условию, АМ=МС по построению. Диагонали четырехугольника АВСD точкой пересечения делятся пополам. ⇒ АВСD – параллелограмм (по признаку).
По свойству параллелограмма сумма квадратов диагоналей равна сумме квадратов ВСЕХ его сторон.
Противоположные стороны параллелограмма равны.
АС²+BD²= 2 АВ²+2ВС²
28²+а²=2а²+6а²⇒
7а²=28•28
а²=4•4•7
а=4√7 см – длина боковых сторон треугольника.
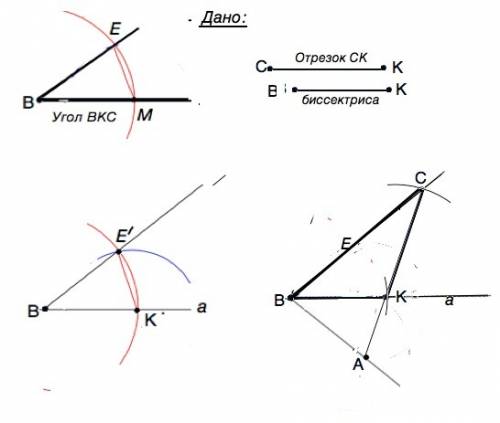
Построение:
Проведем произвольную прямую а. Отметим на ней точку В.
1) Из вершины В данного угла раствором циркуля, равным длине ВК, делаем насечки М и Е на сторонах угла.
2) Соеденим точки М и Е.
3) Отложим на прямой а от В отрезок BК, равный ВМ=биссектрисе ВК.
4) Из точки К проведем полуокружность радиусом, равным отрезку МЕ
5) От В раствором циркуля, равным ВЕ, проведем полуокружность до пересечения с полуокружностью из К
6) Через точку пересечения полуокружностей проведем луч ВЕ'. Данный по условию угол построен.
7) Точно так же построим угол, равный построенному, в другой полуплоскости от прямой а. Получившийся угол равен двум углам ВКС ( в котором ВК - биссектриса)
8) Из К, как из центра, проведем полуокружность радиусом. равным отрезку СК. Точку пересечения с лучом ВЕ' обозначим С.
9) От С через К проведем прямую до пересечения со второй стороной построенного угла ( которая по другую сторону от а).Точку пересечения обозначим А.
10) Треугольник АВС построен. В нем ВК - биссектриса заданной длины, угол СВА=2 угла СВК, КС равен заданному отрезку СК.
1) пусть x - это катет в левой части трапеции с острым углом 30°
пусть y - это катет в правой части трапеции с острым углом 60°
на них приходится 15 - 7 = 8см, следовательно, x + y = 8
выясним, как связаны x и y
tg60 = h / y => y = h / tg60 = h / √3
tg30 = h / x => x = h / tg30 = 3h / √3
заметим, что x > y в 3 раза
пусть x = 3a, y = a
тогда 3a + a = 8,
a = 2
следовательно, x = 6, y = 2
теперь через тот же тангенс найдем высоту трапеции:
tg60 = h / y => h = tg60 y = 2√3.
2) по теореме Пифагора найдем диагонали трапеции
d1 = sqrt(9² + (2√3)²) = √93
d2 = sqrt(13² + (2√3)²) = √181