Сделаем рисунок и обозначим вершины пирамиды АВСА1В1С1. Ребро ВВ1⊥АВС=1 см
Площадь боковой поверхности этой пирамиды - сумма площадей трех трапеций: двух прямоугольных и одной равнобедренной - той, что противолежит ребру ВВ1.
В основаниях пирамиды правильные треугольники - следовательно, длины средней линии всех трапеций равны 0,5•(3+5)=4 см
Площадь прямоугольных граней равна произведению их средней линии на длину высоты пирамиды, т.е. .
S (АВВ1А1)=S (ВВ1С1С)= 4•1=4 см²
Чтобы найти высоту грани АА1С1С, проведем в основаниях пирамиды высоты ВН и В1К и соединим К и Н.
Плоскость прямоугольной трапеции ВНКВ1 перпендикулярна плоскости оснований, т.к. содержит в себе отрезок ВВ1, перпендикулярный обоим основаниям.
Из К опустим высоту КТ.
КН по теореме о трех перпендикулярах перпендикулярна АС и является высотой трапеции АСС1А1.
В прямоугольном треугольнике КТН катет КТ=ВВ1=1см, катет НТ равен разности высот оснований пирамиды.
ВК=(3√3):2
BH=(5√3):2
ТН=2√3):2=√3 см
КН=√(КТ²+НТ²)=√4=2 см
S (АСС1А1)=4*2=8 см²
S(бок)=4+4+8=16 см²

Объяснение:
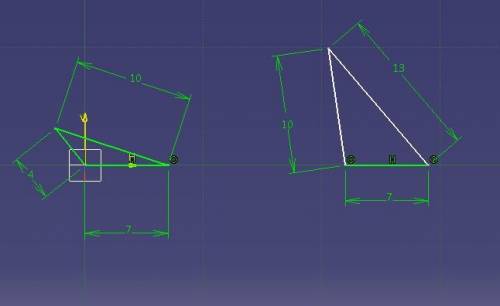
4,7,10,13 см длины проволок.
1. Основное правило существования треугольников: сумма двух любых сторон должна быть больше, чем третья сторона (если нарисовать треугольник, это хорошо видно. Крайний случай, когда один из углов треугольника почти равен 180 град).
Из этого правила.
Возьмем проволоки 4, 7 и 13 cм. Тогда
4+7=11 < 13 (т.е. сумма сторон меньше 3ей, поэтому такого треугольника быть не может)
Возьмем проволоки 4, 7, 10. Тогда
4+7=11 > 10
7+10=17 > 4
4+10=14 > 7
Правило выполняется для любой из сторон, следовательно треугольник существует.
Из проволок можно собрать еще 2 треугольника
{4,10,13}, {7,10,13}, но для них правило выполняется, значит они существуют. Рисунки 2х прикрепил к ответу
прости,писла как курица лапой,быстро