Question

Площадь трапеции. Найдите площадь трапеции её неизвестный элемент.
Любой из этих подчеркнутых задач.​

Answer 1

в) S=30

д) S= скорее всего не хватает данных

ж) S=60

и)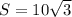 $S=10\sqrt{3}$  

л)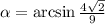 $\alpha=\arcsin\frac{4\sqrt{2}}{9}$

Объяснение:

в) По формуле: площадь трапеции равна полусумме оснований на высоту. Полусумма оснований равна длине серединной линии трапеции.

S=6*5

S=30

д) скорее всего не хватает данных

ж) По формуле площади трапеции, когда диагонали пересекаются по 90°

$S=\frac{d_1*d_2}{2}$

$S=\frac{10*12}{2}$

S=5*12

S=60

и) По формуле площади трапеции

$S=\frac{d_1*d_2}{2}*\sin60^0$

$S=\frac{5*8}{2}*\frac{\sqrt{3}}{2}$

$S=10\sqrt{3}$

л) По формуле площади трапеции

$S=\frac{d_1*d_2}{2}*\sin\alpha$

Подставим известные данные в эту формулу

$48\sqrt{2}=\frac{12*18}{2}\sin\alpha$

$48\sqrt{2}=6*18*\sin\alpha$

$\sin\alpha=\frac{48\sqrt{2}}{6*18}$

$\sin\alpha=\frac{4\sqrt{2}}{9}$

$\alpha=\arcsin\frac{4\sqrt{2}}{9}$