Пирамида SABCD пересечена плоскостью KLNM, параллельной основанию.
1. Каково взаимное расположение прямых (пересекаются, скрещиваются, параллельны):
а) AS и CD? ответ: скрещиваются, т.к. CD∈( ADC) , AS∩( ADC) =A , A∉CD
б) AB и KL? ответ: параллельны , т.к. (KLN)||(АВС).
в) CD и LM? ответ: скрещиваются, т.к.CD∈(CDM) , а LM пересекает эту плоскость в точке М , не лежащей на CD.
2. Как расположены плоскости:
а) ASB и DSC? ответ: пересекаются ,т.к. имеют общую точку
б) ABD и ASD? ответ: пересекаются ,т.к имеют общую прямую.
1)
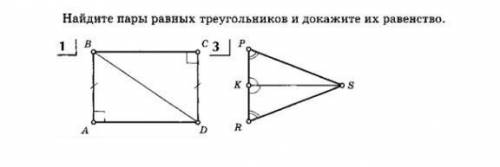
∆ АВС и ∆ СBD
/_ A= /_ C - прямоугольные , по условию
АВ= СD- по условию
ВС= AD - ABCD - прямоугольник
∆ АВС = ∆ СBD
Два треугольника равны, если у них равны две стороны и угол, лежащий между этими сторонами.
2) ∆ SPK и ∆ SRK
/_R= /_ K - по условию
/_ PKS= /_SKR - по условию
РК= КR - SK высота,
потому /_ PKS= /_SKR = 180: 2= 90°
∆ SPK = ∆ SRК
Два треугольника равны, если у них равна одна из сторон и два прилежащих к ней угла