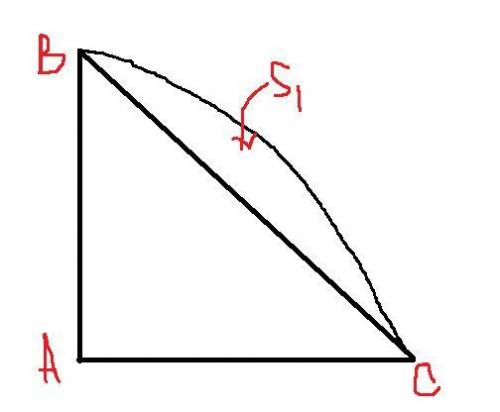
46.5. Искомая площадь вычисляется:
S=S₁-S₂-S₃,
S₁=π(AB)²/8; S₂=π(AD)²/8; S₃=π(DB)²/8.
S=π/8(AB²-AD²-DB²).
Подставим AB=AD+DB, CD²=AD*DB.
S=π/8(AD²+DB²+2AD*DB-AD²-DB²)=π*AD*DB/4 = π*CD²/4.
46.4. Рассмотрим четверть квадрата (Рис. ниже) со стороной a. Найдем S₁.
S₁=Sсек -Sтреуг, где Sсек - площадь сектора круга, ограниченного радиусами AB и AC, Sтреуг - площадь треугольника ABC.
Sсек = Sкр/4 = πa²/16.
Sтреуг = a²/8.
S₁ = a²/8*(π/2-1).
Искомая площадь: S=8*S₁ = a²*(π/2-1). По условию a=4 см.
S = 16(π/2-1) см.
46.6. Площадь (из задачи 46.5) вычисляется:
S=π*CD²/4 = π*AD*DB/4 = π*6*4/4 = 6π см².
Длина дуги окружности диаметра AB: L₁=πAB/2=5π см.
Длина дуги окружности диаметра AD: L₂=πAD/2=3π см.
Длина дуги окружности диаметра DB: L=πDB/2=2π см.
Периметр: L=L₁+L₂+L₃ = 5π+3π+2π = 10π см.
Объяснение:
1) Осевая симметрия.
Из точки D надо с омощью линейки и угольника провести перпендикуляр к прямой L, продлив его за прямую L, отметить прямой угол и , замерив расстояние от точки D до прямой L, отступить по перпендикуляру в другую сторону от прямой L такое же расстояние. Это удобно делать циркулем. Показать штрихом равные отрезки. Получим точку D₁.
Также поступить с точками С и Е. Получим C₁ и E₁ (полученный треугольник С₁Е₁D₁ лучше чертить цветным карандашом).
2) Центральная симметрия.
Из точки А провести луч через точку О. Замерить циркулем расстояние от О до А и отступить такое же расстояние в другую сторону от точки О. Получим точку А₁. Показать штрихом равенство двух отрезков АО и ОА₁. Аналогично отработать с точками В и С. Получим точки В₁ и С₁. Точки А₁ ,В₁ ,С₁ соединить цветным карандашом.
3) Параллельный перенос.
Из точек Р, М и К провести с линейки и угольника вправо лучи параллельно заданному вектору "а". Замерить циркулем длину вектора "а" и от каждой из этих точек отступить такие же расстояния.
Получим точки Р₁ ,М₁ и К₁. Соединим эти точки цветным карандашом.
6 см
Объяснение:
Против угла 30° лежит половина гипотенузы. Bc= 12/2=6см.