Объем цилиндра равен произведению его высоты на площадь основания.
V=Sh
Формула площади основания цилиндра= формула площади круга:
S=πr²
Диаметр основания по условию 6см, следовательно, его радиус равен 3 см.
S=π3²=9π cм²
V=9π ·12=108π см² или 339,29 см³ ( на π умножала в калькуляторе без его округления)
угол MBC = 30°
угол ВCA = 60
Объяснение:
Дано:
АВС - треугольник
АМ = СМ
уг. АВС = 60°
уг. ВМА = 90°
-------------
Найти
уг. МВС - ?
уг. ВСА - ?
Решение
угол ВМА = 90° => уг. ВМС = 90°
т.е. ВМ | АС, а значит,
ВМ - высота, проведенная из вершины В на АС.
Также АМ = МС, а значит
ВМ - медиана, проведенная из вершины В на АС.
Если медиана треугольника является его высотой, то этот треугольник - равнобедренный.
ВМ - высота и медиана ∆АВС, =>
=> ∆АВС - равнобедренный, основание АС =>
=> ВМ - также является биссектрисой ∆АВС, т.е.
уг. АВМ = уг. СВМ
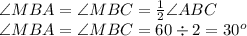
Так, как ∆АВС - равнобедренный, с основанием АС, то углы при основании - равны друг другу
уг. ВАС = уг. АСВ
и равны
угол ВАС = угол ВСА = 1/2 • (180 - угол АВС)
угол ВАС = угол ВСА = 1/2 • (180 - 60) = 60°
а значит ∆АВС - равносторонний.
угол MBC = 30°
угол ВCA = 60°
дано: паралелограм ABCD построен на векторах а и b как на сторонах. Известно, что модуль вектора а равен 3, модуль вектора b равен 5, модуль векторов а+b равен 7.
найти: величину угла между векторами a и b(в градусах)
Объяснение:
Дано: ABCD- параллелограмм, построен на векторах а и b как на сторонах. Известно, что модуль вектора| а |=3, | b|=5, | а+b|=7.
Найти: величину угла между векторами a и b
Решение
Пусть АВ=а (вектора), ВС=b(вектора). Тогда суммой двух векторов, по правилу треугольника АВ+ВС=АС (вектора). По условию АВ+ВС=а+b(вектора), поэтому
АС= а+b(вектора), а |АС|= |а+b|=7 (вектора).
В ABC вектора ВС=АД .Тогда углом между векторами а и b будет ∠ВАD=180°-∠АВС.
ΔАВС, АВ=3,ВС=5, АС=7.
По т. косинусов :
АС²=АВ²+ВС²-2*АВ*ВС*cosВ,
49=9+25-30*cosВ,
cosВ=-0,5
∠В=120 , а значит ∠ВАD=180°-120°=60°.
ответ: 339,12см^3