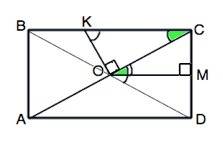
Срединный перпендикуляр диагонали АС прямоугольника АВСD пересекает сторону ВС и образует с ней угол, равный углу между диагоналями. Найдите этот угол.
Срединный перпендикуляр проведен к точке пересечения диагоналей, которая делит их пополам.
Обозначим его ОК.
Треугольник КОС - прямоугольный.
Боковые стороны треугольника СОD образованы равными половинами диагоналей, следовательно, он - равнобедренный.
Проведем в нем высоту ОМ, она же – биссектриса ( свойство равнобедренного треугольника) и делит угол COD пополам.
ОМ║КС ( углы КСМ=ОМС=90°)
∠ МОС=∠ОСК - накрестлежащие при пересечении параллельных прямых секущей. .
Но угол МОС - половина угла СОD, который равен углу СКО.
Следовательно, ∠КОС=2 ∠КСО.
Сумма углов прямоугольного треугольника равна 90°
Угол КСО=2 КСО=90°
∠КСО=90°: 3=30°
∠ СКО=60°
Треугольник правильный, значит, у него все стороны равны. Обозначим сторону треугольника за а. Периметр будет равен 3а, а площадь будет равна высоте, умноженной на 0,5а. По теореме Пифагора в прямоугольном треугольнике, где катетами является эта высота и 0,5а, а гипотенуза равна а, имеем, что высота равна 0,5а*корень из 3. Радиус равен отношению площади к периметру, значит, 3=3а*0,5а*корень из 3, откуда выражаешь а, а затем считаешь площадь и периметр :)
Удачи :)