1. объемы до и после распила одинаковые
V=n*v
v=1/4a*1/4b*1/4c
2. тоже самое
3.Vтр призмы=Sтр основания*H
Плоскость, проходящая через средние линии будет параллельна боковой грани призмы, по паре параллельных прямых. Значит фигура бкдет разделена на две - треугольную призму и четырехугольную с трапецией в основании. Причем, высоты призм одинаковы и равны H.
Далее задача сводится к нахождению отношения оснований треугольной и трапецивидной призмы, а точнее отношению площадей их оснований - треугольника и трапеции.
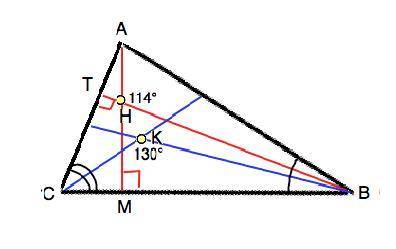
Треугольник ABC остроугольный. Высоты, проведенные из вершин A и B, пересекаются в точке H, образуя угол AHB = 114°. Биссектрисы углов B и C пересекаются в т. K, образуя угол BKC= 130°. Найдите градусную меру всех углов треугольника АВС.
Решение.
1) В ∆ ВКС ∠КВС+ ∠КСВ=180°-130°=50° (из суммы углов треугольника)
∠КВС= 0,5 ∠АВС;
∠КСВ=0,5 угла КСВ ⇒ их сумма равна 0,5•(∠АВС+∠АСВ) ⇒
∠АВС+∠АСВ=2•50°=100°. Тогда ∠ВАС=180°-100°=80°
2) Обозначим высоты ВТ и АМ.
Сумма острых углов прямоугольного треугольника 90°.
В ⊿ АВТ ∠АВТ=90°-угол А=90°-80°=10°
В ⊿ ВНМ ∠ВНМ=180°-114°=66° ( смежный угу МНТ) ⇒
∠НВМ=90°-66°=24° ⇒
∠АВС=∠АВТ+∠НВМ=10°+24°=34° ⇒
∠ВСА=180°-∠А-∠В=180°-80°-34°=66°
Воспользуемся расширенной теоремой синусов, чтобы узнать радиус описанной окружности
Сократим обе части на 2 и получим длину радиуса описанной окружности
Длины сторон треугольника ВОС равны
По формуле Герона вычислим площадь треугольника ВОС
Сначала вычислим полупериметр
ответ: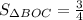 - квадратных единиц.
- квадратных единиц.