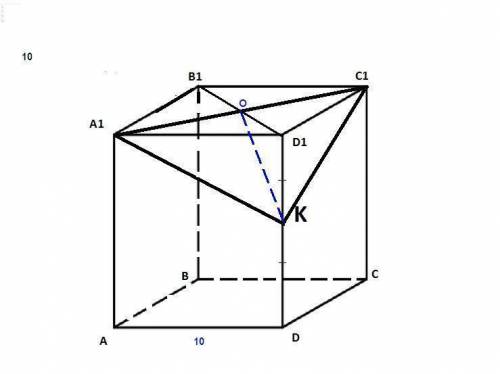
Соединяем точки А₁, С₁ и К, так как они попарно лежат в одной грани.
А₁С₁ = 10√2 как диагональ квадрата.
ΔА₁D₁K: по теореме Пифагора
А₁К = √(A₁D₁² + D₁K²) = √(10² + 5²) = √125 = 5√5
ΔA₁D₁K = ΔC₁D₁K по двум катетам (A₁D₁ = C₁D₁ как ребра куба, D₁K - общий), значит А₁К = С₁К = 5√5
Рa₁c₁k = 10√2 + 5√5 + 5√5 = 10√2 + 10√5 = 10(√2 + √5).
КО - медиана и высота равнобедренного треугольника А₁С₁К.
По теореме Пифагора:
КО = √(А₁К² - А₁О²) = √(125 - (5√2)²) = √(125 - 50) = √75 = 5√3
Sa₁c₁k = 1/2 · A₁C₁ ·KO = 1/2 · 10√2 · 5√3 = 25√6
Задача "Найдите сторону основания пирамиды" без уточнения какая именно пирамида ---некорректна...
Можно предположить, что стороны основания равны (т.к. ничего не сказано о их отличиях...)
т.е. допускаем, что в основании равносторонний треугольник...
и предположим, что пирамида правильная (об этом тоже ничего не сказано...), т.е. основание высоты пирамиды попадает в центр треугольника АВС...
обозначим пирамиду SABC, SK ---апофема боковой грани, ВК ---высота и медиана основания, SO ---высота пирамиды...
tg(SKB) = 7.5 = SO / KO (по определению тангенса)
SO = 7.5*KO = 30*V3
KO = 30*V3 / 7.5 = 4*V3
если в основании правильный треугольник, то О делит медианы в отношении 2:1, считая от вершины, т.е. ОК = ВК/3
ВК = 3*ОК = 12*V3
медиана равностороннего треугольника = а*V3 / 2, где а ---сторона треугольника
12*V3 = а*V3 / 2
a = 24 ---искомая сторона основания...