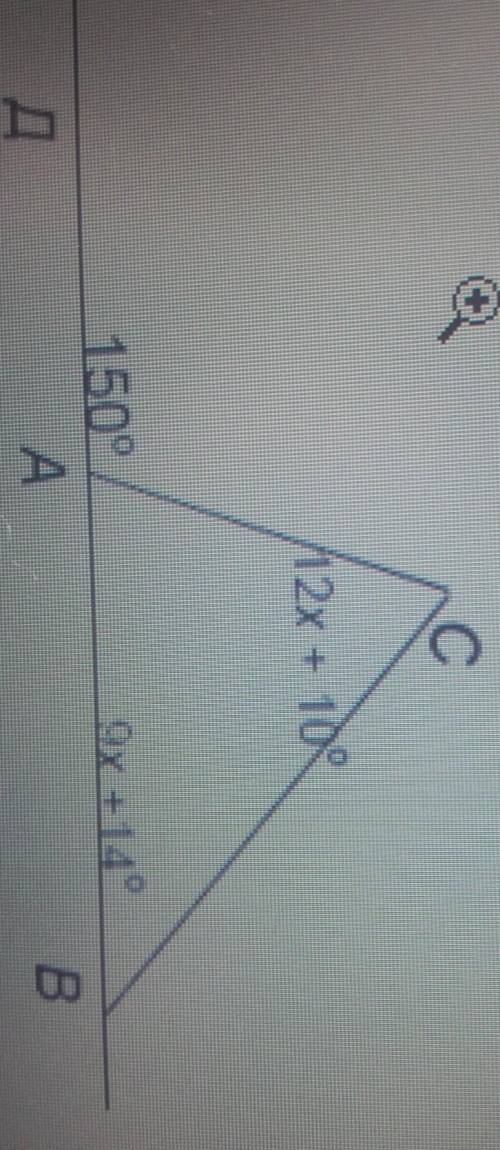
∠С 82° и ∠В 68°
Объяснение:
Теорема о внешнем угле треугольника гласит:
внешний угол треугольника равен сумме двух других углов, не смежных с ним. На основании этой теоремы можно составить уравнение:
150° = (12х+10°) + (9х+14°). Приведем подобные:
150 = 21х + 24
126 = 21х. Найдем х:
х = 126/21 = 6°.
Теперь можно вычислить углы.
∠С = 12*6 + 10 = 72+10 = 82°
∠В = 9*6 + 14 = 54 + 14 = 68°
Чертеж с дополнительными построениями не нужен, достаточно приложенного к задаче.
Объем пирамиды равен одной трети произведения площади основания на
высоту.
V=1/3·h·S
Высота дана в условии и равна √3.
Площадь основания найдем по формуле
S=a²√3):4
Сторона основания а.
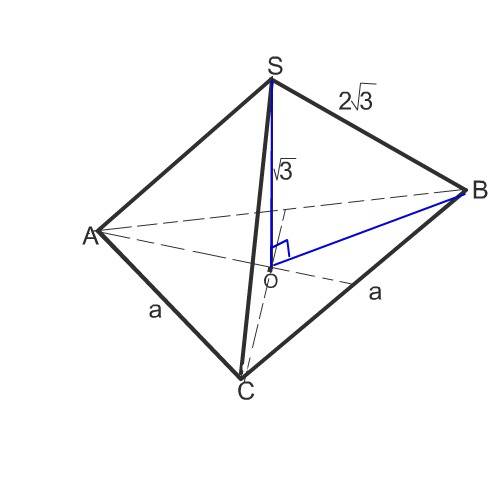
Основание высоты пирамиды находится в точке О пересечения ее медиан ( высот, биссектрис) и делит их в отношении 2:1, считая от вершины.
Ребро пирамиды SB, ее высота SO и 2/3 медианы (высоты) BO основания образуют прямоугольный треугольник SBO с гипотенузой SB.
Из этого треугольника найдем сторону а основания.
2/3 медианы = 2/3 от а√3):2 ( формула высоты правильного треугольника) и равны 2а√3):6=а√3):3
SB²=SO²+OB²
(2√3)²=(√3)²+(а√3):3)²
12= 3 + 3а² :9
108=27+3а²
3а²=81
а²=27
S=a²√3):4=27√3):4
V=1/3·√3·27√3):4)= 27:4= 6,75 ( кубических единиц измерения)
радиус окружности описанной возле правильного треугольника находится по формуле : R=корень из 3 делить на три и умноженный на сторону треугольника
R=корень из 3 деленный на три умножаем на 4 корня из 6
R=корень из 288 деленного на 3
R=12 корней из 2 и все это делить на 3
R=4 корня из 2
далее находим сторону квадрата вписанного в эту же окружности
радиус окружности треугольника равен радиусу окружности квадрата
радиус квадрата равен R=корень из 2 деленный на 2 и все это умножить на сторону квадрата (t)
выражаем t из этой формулы получаем
t= R делить на корень из 2 деленный на 2
t=4корня из 2 делить на корень из 2 деленный на 2
t=8 см
ответ: 8 см.
12x+10+9x+14= 150 (по теореме о внешнем угле)
21x = 126
x = 6
тогда угол В = 9*6+14 = 68