
В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой острого угла при основании. Найти высоту трапеции , если ее площадь равна 9√3
Объяснение:
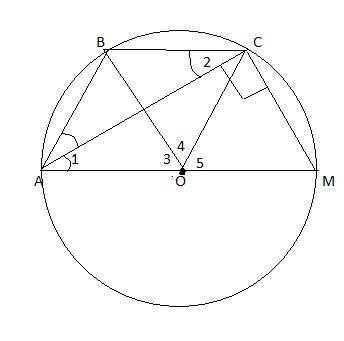
АВСМ-равнобедренная трапеция.
1)Если трапеция является равнобедренной, то около неё можно описать окружность. Пусть О-принадлежит АМ . Тогда ОА=ОС=ОМ как центры описанной окружности , т. к. центр описанной окружности лежит на середине гипотенузы .
2)Углы 1 и 2 равны как накрест лежащие при АМ||ВС, АС-секущая⇒ΔАВС-равнобедренный и ВА=ВС. Значит и ВА=ВС=МС.
3)ΔОАВ=ΔОВС=ΔОСМ по трем сторонам ВА=ВС=МС, остальные радиусы......Значит
- ∠3=∠4=∠5=180°:3=60°.
- их площади равны и S(ΔОСМ )=9√3:3=3√3.
3)В ΔОСМ ,∠СОМ=60° и ОС=ОМ ⇒ два других угла по 60°⇒этот треугольник равносторонний.
S( равност.тр)=(а²√3):4 .Найдем сторону треугольника (а²√3):4=3√3 или а²=12 , а=√12 .
Площадь можно найти иначе S( равност.тр)=1/2*а*h.
3√3=1/2*√12*h или h=3.
Правильная четырёхугольная призма.
АС1 = l
Диагональ АС1 образует с плоскостью основания угол.
Найти:S боковой поверхности - ?
Решение:Так как данная призма - четырёхугольная, правильная => основание данной призмы - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
А все боковые грани - прямоугольники.
Угол между диагональю и плоскостью основания - угол между диагональю и её проекцией на плоскость основания.
Проекцией диагонали АС1 на плоскость основания - это диагональ BC квадрата ABCD => ∠С1АС - угол, образованный между диагональю АС1 и плоскостью основания ABCD.
Так как AC1 = I => AC = I * cos∠C1AC;
CC1 = h призмы = l * sin∠C1AC
Так как ABCD - квадрат => АС = АВ * √2 => AB = AC/√2 => AB = l * cos∠C1AC/√2 = I * √2 * cos∠C1AC/2.
S бок поверхности = Р * h, где Р - периметр основания; h - высота призмы.
Р = 4АВ = 2 * l * √2 * cos∠C1AC.
=> S бок поверхности = (2 * l * √2 * cos∠C1AC) * (l * sin∠C1AC) = 2√(2)l² * cos∠C1ACsin∠C1AC = sin(2∠C1AC) * √(2)l² = √(2)l² * sin(2∠C1AC) = l²√(2)sin(2∠C1AC)
ответ: l²√(2)sin(2∠C1AC).