ответ: 76π см²
Объяснение: Трапеция АВСД, вращаясь около бóльшего основания AD, образует тело вращения - цилиндр с «уложенным» на него конусом, одно из оснований которых – общее.
Площадь поверхности этого тела состоит из площади боковой поверхности конуса, площади боковой поверхности цилиндра и площади основания цилиндра.
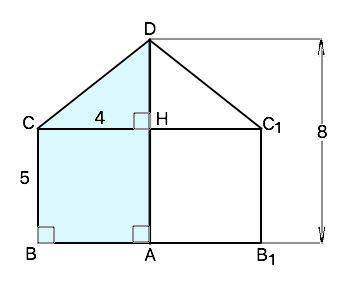
На рисунке приложения дано осевое сечение фигуры.
Радиус основания - высота трапеции СН. Образующая конуса - боковая сторона CD трапеции АВСD. Высота цилиндра - меньшее основание.
☐ АВСН - прямоугольник, АН=ВС=5 ⇒ DH=AD-АH=8-5=3 см
Из ⊿ CHD по т.Пифагора СD=√(CH²+DH²)=√(4²+3²)=5.
S бок. кон=πrL=π•4•5=20π см²
Ѕ бок. цил.=2πr•h=8π•5=40π см²
Ѕ осн. цил. =πr*=16π см²
S полн=20π+16π+40π=76π см²
Поскольку наклонные, являющиеся расстояниями от М до сторон тр-ка, одинаковые, то и проекции их на плоскость треугольника одинаковые и равны радиусу вписанной в треугольник окружности.
r = √((р - а)(р - в)(р - с)/р
Пусть а = 25, в = 39, с = 56, тогда полупериметр
р = 0,5·(25 + 39 + 56) = 0,5·120 = 60
r = √((60 - 25)(60 - 39)(60 - 56)/60) = √(35·21·4/60 = √49 = 7
Растояние Н от точки М до плоскости тр-ка, радиус r вписанной окружности и любая из наклонных L = 25 образуют прямоугольный тр-к с гипотенузой L.
По теореме Пифагора найдём Н
Н² = L² - r² = 25² - 7² = 625 - 49 = 576
Н = 24(см)