1) Дано:
<СВА = <DBA
DB = CB.
Док-ть:
∆АСВ = ∆ADB
Док-во:
Рассмотрим ∆АСВ и ∆ADB.
АВ - общая сторона.
<СВА = <DBA, DB = CB, значит ∆АСВ = ∆ADB по | признаку (по двум сторонам и углу между ними).
5) Дано:
QK = FP, QM = MP, KM = MF
<KQM = <FPM
Док-ть:
∆QFM = ∆KMP;
∆QKM = ∆FMP;
∆QPK = ∆QPF;
∆KQF = ∆KFP;
Док-во:
QK = FP, QM = MP, KM = MF, значит КQFP - параллелограмм.
<KQM = <FPM
1) Рассмотрим ∆QFM и ∆KMP.
<KMP = <QMP как вертикальные
QM = MP, KM = MF, значит ∆QFM = ∆KMP по | признаку.
QF = KP по св-ву параллелограмма, значит ∆QFM = ∆KMP по ||| признаку.
∆QFM = ∆KMP по | и ||| признакам.
2) Рассмотрим ∆FMP и ∆QMK.
<FMP = <QMK как вертикальные.
QK = FP, KM = MF, QM = MP, значит ∆FMP = ∆QMK по | и ||| признакам.
3) Рассмотрим ∆KQP и ∆QFP.
QK = FP, QP - общая сторона
KP = QF по св-ву параллелограмма.
<KQM = <FPM
<QKP = <QFP по св-ву параллелограмма, значит ∆KQP = ∆QFP по | , || , ||| признакам.
4) Рассмотрим ∆KQF и ∆KFP.
KF - общая сторона.
QK = FP, QF = KP.
<KQF = <FPK.
∆KQF и ∆KFP по | , || , ||| признакам.
ч.т.д
Дано:
усеченный конус
r = O₁B = 5 см
R = OA = 11 см
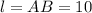см
-----------------------------
Найти:
Sсеч - ?
1) Проведем BH⊥AO.
OH = O₁B = r = 5 см
AH = OA - OH = R - r = 11 см - 5 см = 6 см
2) Рассмотрим ΔAHB:
BH⊥AO | ⇒ ΔAHB - прямоугольный
∠AHB = 90° |
AB² = AH² + HB² - по теореме Пифагора, следовательно: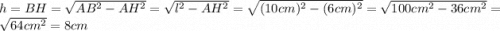
h = BH = OO₁ = 8 см
3) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: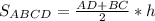 
4) В трапеции ABCD:
AD = 2AO = 2R = 2×11 см = 22 см h = BH= 8 см
BC = 2BO₁ = 2r = 2×5 см = 10 см
5) Тогда площадь трапеции равна:
⇒
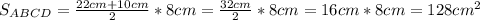Sсеч = 
= 128 см²
ответ: Sсеч = 128 см²
P.S. Рисунок показан внизу↓
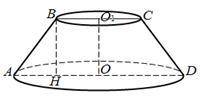
1) отрезок, соединяющий середины диагоналей, равен полуразности оснований. С другой стороны, он же является частью средней линии.
2) Пусть основания трапеции a и b. Тогда: (a-b)/2=12.
3) Т.к. средняя линия равна полусумме оснований, то (a+b)/2=24 (по условию)
4) Из двух вышеприведённых равенств составим систему: {a-b=24; a+b=48}. 2a=72; a=36; b=12
5) треугольники KAN подобен LAM (KN||LM)
6) LN/KN = 12/36 = 1/3; AL/AK = AM/AN = 1/3 (из подобия)
7) AK - AL = 10; AN - AM = 26 (боковые стороны в условии)
8) Из (6) и (7): AL=5; AM=13
9) треугольник ALM - прямоугольный (его стороны 5; 12 и 13 удовлетворяют теореме Пифагора)
10) Радиус вписанной в прямоугольный треугольник окружности равен:
r=(a+b-c)/2, в нашем случае: r=(5+12-13)/2=4/2=2