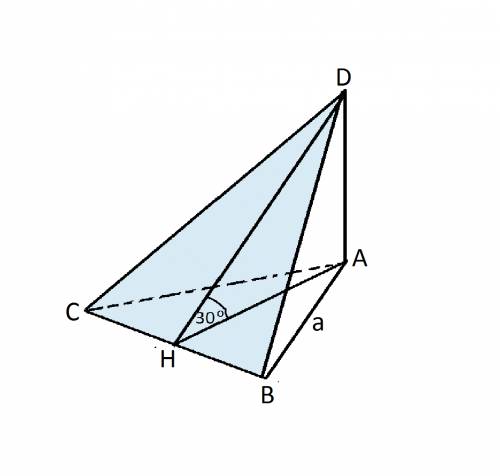
1.Проведём АН -медиану правильного треугольника АВС. Она перпендикулярна стороне ВС, т.к. медиана правильного треугольника одновременно является его высотой.
2.В треугольнике АНС угол Н равен 90 град, сторона АС равна а (по условию), сторона НС равна а/2, т.к. АН-медиана АВС.
АН= sqr(a^2- (a/2)^2)=sqr((3a^2) /4)=(a*sqr3) / 2
3.В треугольнике ДАН угол А равен 90 град, т.к. ДА препенд. пл-ти АВС., угол Н равен 30 град, НА =(a*sqr3) / 2.
Найдём ДА через tg угла ДНС:
tg 30 = ДА / (a*sqr3) / 2, отсюда ДА= а/2
4.Найдём площадь боковой поверхности пирамиды:
S=S(ДАС)+ S(ДАВ)+S(СВД)
S(ДАС)=1/2*АС*АД=1/2*а*а/2=a^2 /4
S(ДАВ)=S(ДАС)=a^2 /4
S(СВД)=1/2*ВС*ДН
ДН найдём из треугольника ДНС ДН= ДА / sin 30= (a/2): 1/2=a
S(СВД)=1/2*a*a=1/2*a^2
S = 2*(a^2 /4) + a^2 /2 = a^2
условие сформулировано так, что могут быть 2 ответа - в зависимости от того, какая из вершин АС - А или С является вершиной прямого угла треугольника АВС. Предположим, что это - С.
Тогда треугольник АВС "египетский", стороны (6,8,10). (это я не навязчиво нашел второй катет АВС, ВС = 6)
Угол между плоскостью b и плоскостью АВС - это угол между катетом ВС = 6 и его проекцией на b. Обозначим проекцию точки В на b как М. Тогда треугольник ВМС прямоугольный, ВС = 6 и угол МСВ = 30 градусов, откуда ВМ = 3. (это ответ)
В том случае, если вершиной прямого угла является А, принцип решения тот же, но - еще проще, поскольку нам нет необходимости искать третью сторону АВС, Поскольку АВ - тоже катет, и искомый угол как раз между ним и b, то есть расстояние в этом случае равно АВ/2 = 5. (это другой ответ, посмотрите, какое из условий правильное, и выбирайте. Но задачи эти разные, и как мне кажется, правильное условие - первое.)