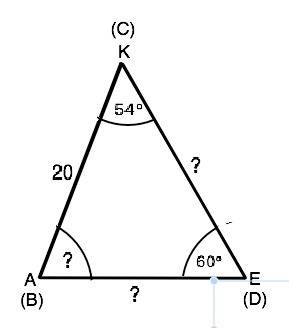
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
В правильной треугольной пирамиде в основании лежит равносторонний
треугольник со стороной а = 10см.
Sбок = Росн*h Росн = а+а+а = 3а Н = 15см высота пирамиды
h высота боковой грани h = V(H^2 + r^2) r = aV3/6 радиус вписанной окружности
равностороннего треугольника h =V(15^2 + 10^2 *3/36 = V(225 + 25/3) = 10V(7/3)
Sбок = 3*10*10V(7/3) = 100V21(см^2)
Vпир=1/3*Sосн * H Sосн = a^2V3/4
Vпир = 1/3 *10^2 *V3/4 = 25/3V3 (см^3)