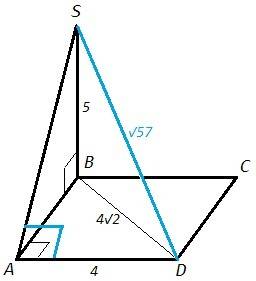
Прямая SB перпендикулярна двум пересекающимся прямым в плоскости ABC, следовательно перпендикулярна плоскости и любой прямой в этой плоскости. SB⊥BD. BD=4√2 (диагональ квадрата). По теореме Пифагора:
SD= √(SB^2 +BD^2) =√(25+32) =√57
SB⊥BA, BA - проекция SA. Теорема о трех перпендикулярах: если прямая (AD), проведенная на плоскости через основание наклонной (SA), перпендикулярна ее проекции (AD⊥BA), то она перпендикулярна и самой наклонной (AD⊥SA). △SAD - прямоугольный.
Проверка:
SA= √(SB^2 +AB^2) =√(25+16) =√41
57=41+16
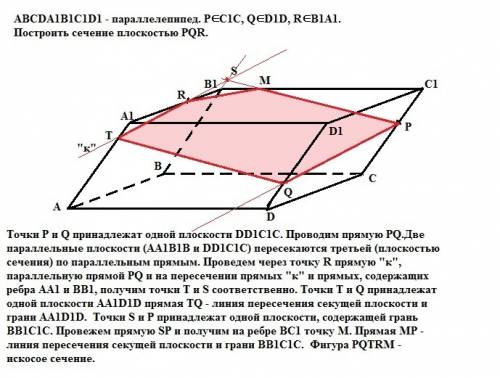
Точки Р и Q принадлежат одной плоскости DD1C1C. Проводим прямую PQ.Две параллельные плоскости (АА1В1В и DD1C1C) пересекаются третьей (плоскостью сечения) по параллельным прямым. Проведем через точку R прямую "к", параллельную прямой PQ и на пересечении прямых "к" и прямых, содержащих ребра АА1 и ВВ1, получим точки Т и S соответственно. Точки Т и Q принадлежат одной плоскости АА1D1D прямая ТQ - линия пересечения секущей плоскости и грани АА1D1D. Точки S и P принадлежат одной плоскости, содержащей грань ВВ1С1С. Провежем прямую SP и получим на ребре ВС1 точку М. Прямая МР - линия пересечения секущей плоскости и грани ВВ1С1С. Фигура PQTRM - искомое сечение.
"Вспоминаем" подходящие формулы.
Радиус окружности, вписанной в равнобедренный тр-к:
r = b/2* √(2a-b)/(2a+b), где b - основание, а - боковая сторона.
b = 2aCosα, где b - основание, а - боковая сторона, α - угол между ними.
Площадь S=1/2*a*b*Sinα
Вставляем известные величины: r = (2aCosα/2)*√(2a-2aCosα)/(2a+2aCosα) =
aCosα√[(1-Cosα)/(1+Cosα)]. Тогда а=r/(Cosa*√[(1-cosa)/(1+cosa)])=r/(cosa√[sin^2a/(1+cosa)^2]=r(1+cosa)/(cosa*sina).
b = 2a*Cosa
S = (1/2)*a*b*Sina=(1/2)*r(1+cosa)*2a*cosa*sina)/(cosa*sina)=r(1+cosa)*r*(1+cosa)/(cosa*slna) = r^2*(1+cosa)^2/(cosa*sina)=r^2*(1+2cosa+cos^2a)/(cosa*sina).
Sin30=1/2. Cos30=√3/2. Тогда
S=r^2*4*(4+4√3+3)/(√3*4)=r^2*(7+4√3)/√3 = 8,005*r^2 =~8r^2.
ответ: S = 8r^2.