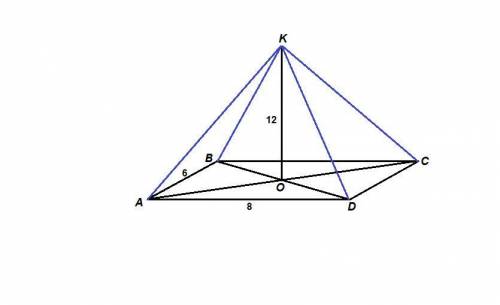
KA = KB = KC = KD = 13
Объяснение:
Из прямоугольного треугольника АВС находим АС по теореме Пифагора:
АС = √(АВ² + ВС²) = √(36 + 64) = 10
Диагонали прямоугольника равны и точкой пересечения делятся пополам:
АО = ВО = СО = DO = 5
АО, ВО, СО и DO - проекции наклонных KA, KB, KC и KD на плоскость прямоугольника.
Если равны проекции наклонных, проведенных из одной точки, то равны и сами наклонные, т.е.
KA = KB = KC = KD.
Из прямоугольного треугольника АОК по теореме Пифагора находим КА:
КА = √(ОК² + АО²) = √(12² + 5²) = √(144 + 25) = √169 = 13
KA = KB = KC = KD = 13
АА1-биссектриса угла А треугольника АВС, следовательно, по свойству биссектрисы треугольника, АС:СЕ=АВ:ВЕ
АС:5=14:ВЕ
АС*ВЕ=5*14=70
Для треугольника АВЕ высотой является катет АС треугольника АВС, поэтому
S(АВЕ)=ВЕ*АС/2=70/2=35