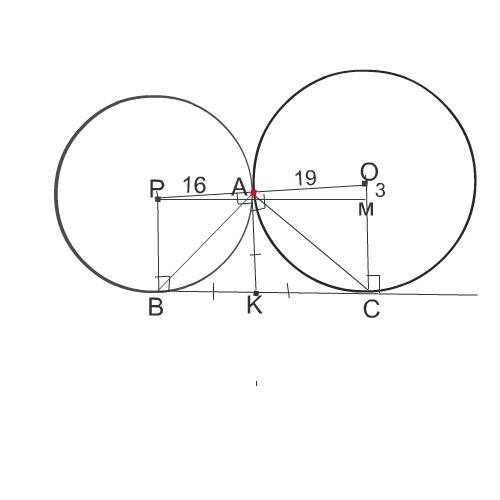
Рассмотрим рисунок.
Точка К - точка вне окружностей, из которой к каждой из них до точек касания В и А к меньшей и до точек С и А к большей идут одинаковой длины отрезки.(по свойству равенства отрезков касательных из одной точки)
КВ=КА.
КА=КС.
ВК=КС
Проведем из центра Р меньшей окружности к радиусу ОС большей окружности перпендикуляр РМ.
Отрезок ОМ равен разности между радиусами окружностей и равен 19-16=3 см
РМ=ВС
РМ по теореме Пифагора из треугольника РОМ равно 8√19
ВК=КС=8√19:2=4√19
АК=ВК=4√19
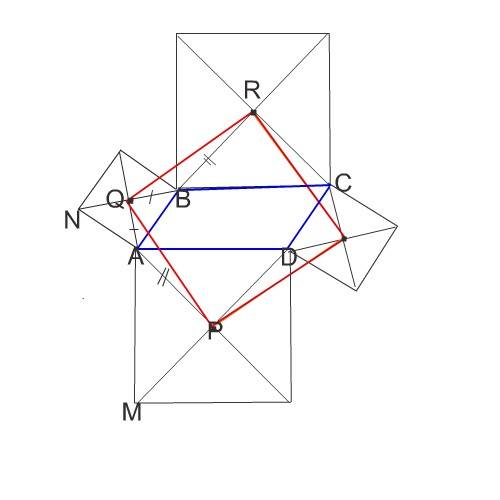
Сделаем рисунок.
Обозначим буквами P, Q и R центры квадратов, построенных на сторонах DA, AB и BC параллелограмма.
Острый угол при вершине A обозначим α.
∠ PAQ = 1/2∠DAM +1/2∠BAN+ α = 90º+α
∠ RBQ=360º-(180º-α) - 90º=180º- 90º+α=90º+α .
∠ PAQ =∠ RBQ
QB=AQ, BR=AP как половины равных диагоналей, а значит,
Δ PAQ = Δ RBQ.
PQ=RQ.
Стороны AQ и BQ этих треугольников перпендикулярны, поэтому PQ ⊥ QR.
Так же доказывается перпендикулярность других углов четырехугольника с равными сторонами.
Центры построенных на сторонах параллелограмма квадратов являются вершинами квадрата.
Объяснение:
sinA= CB/AB
СВ найдем по теореме Пифагора ( 13²-5²=144=12)
sin A = 12/13
____
cos A = AC/AB =5/13
____
tg A= CB/AC=12/5= 2 2/5
___
ctg A= AC/CB=5/12
Угол В:
sin B = AC/AB=5/13
____
cos B = CB/AB=12/13
____
tg B = AC/CB= 5/12
____
ctg B = CB/AC= 12/5= 2 2/5