Из за того, что один из отрезков равен радиусу, угол треугольника с вершиной в конце этого отрезка - прямой (там получается ромб из 2 отрезков касательных и из 2 радиусов, ясно что это квадрат, поскольку углы между касательными и радиусами в точки касания прямые).
Для прямоугольного треугольника стороны a = 4 + 5 = 9; b = x + 4; c = x + 5; связаны теоремой Пифагора. (x - единственный неизвестный из отрезков, на которые точки касания вписанной окружности делят стороны)
(x + 4)^2 + 9^2 = (x + 5)^2;
4^2 + 9^2 - 5^2 = 2*x;
x = 36;
Стороны 9, 40, 41, это известная Пифагорова тройка (наподобие 3,4,5 или 5,12,13)
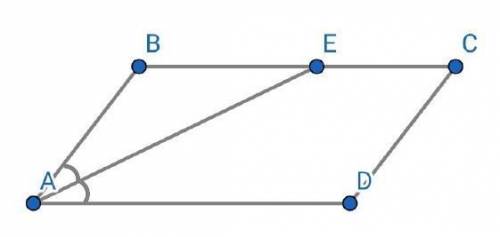
Четырёхугольник ABCD — параллелограмм.
Отрезок АЕ — биссектриса ∠А.
Е ∈ ВС.
ВЕ = 3*ЕС.
ВС = 12 [см].
Найти :Р(ABCD) = ?
Решение :Пусть ЕС = х, тогда, по условию задачи, ВЕ = 3х.
ВС = ВЕ + ЕС
12 [см] = 3х + х
4х = 12 [см]
х = 3 [см].
ВЕ = 3х = 3*3 [см] = 9 [см].
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.Следовательно, ∆АВЕ — равнобедренный (причём ВЕ = АВ = 9 [см]).
Периметр параллелограмма равен удвоенной сумме его смежных сторон.Следовательно, Р(ABCD) = 2*(AB + BC) = 2*(9 [см] + 12 [см) = 2*21 [см] = 42 [см].
ответ :42 [см].
х(х+16)=15^2
x^2+16x-225=0
D=34^2
x1=-25
х2=9
Гипотенуза 9+16=25
Второй катет равен корень (25*16)=5*4=20
Радиус окружности-r
r=(a+b-c)/2.
r=(15+20-25)/2=5
2) r=(a+b-c)\2
Радиус описанной вокруг прямоугольного треугольника окружности равен R=c\2
a, b-катеты, c - гипотенуза
с=2*5=10
a+b=2*2+10=14
a^2+b^2=c^2
a^2+b^2=10^2=100
a^2+b^2=(a+b)^2-2ab=100
14^2-2ab=100
2ab=96
ab=48
a+b=14
ab=48
(6+8=14; 6*8=48)
a=6 b=8 или a=8, b=6
ответ: длины катетов 6 и 8
3)Квадрат отсекает вверху от большего треугольника меньший равносторонний, со сторонами равными m А вторую часть стороны найдем из прямоугольного треугольника, где гипотенуза - оставшаяся часть стороны треугольника, катеты - вертикальная сторона квадрата m и часть основания ( не нужна.) Гипотенуза равна m деленное на синус 60.
И складываете.m: sin(60°)+m =m(2√3+3):3