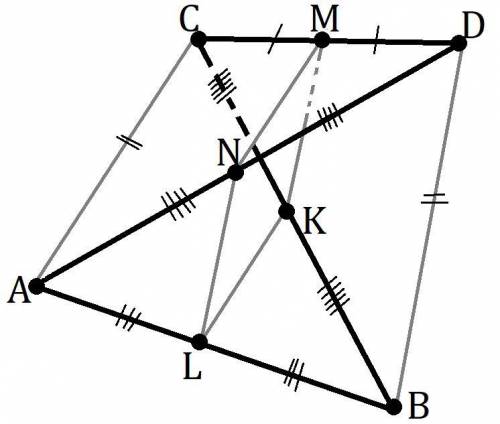
Дано: D∉(ABC); AC=BD; AL=LB (L∈AB); BK=KC (K∈BC); CM=MD (M∈CD); DN=NA (N∈DA).
Доказать: MNLK - ромб.
AC║MN и AC=2MN т.к. MN - средняя линия ΔACD.
AC║LK и AC=2LK т.к. LK - средняя линия ΔACB.
MN║AC║LK ⇒ MN║LK; 2MN=AC=2LK ⇒ MN=LK
MN║LK ⇒ MN, LK ⊂ (MNL), в этой плоскости рассмотрим четырёхугольник MNKL: у него две противоположные стороны параллельны и равны (MN, LK),поэтому это точно параллелограмм у ромба помимо этого ещё все стороны равны, значит чтобы доказать, что MNLK - ромб осталось только доказать, что MK=NM т.к. если это выполняется, то NL=MK - как противоположные стороны параллелограмма, а значит MN=NL=LK=KM.
BD=2MK т.к. MK - средняя линия ΔBDC.
BD=AC - по условию.
2MK=BD=AC=2MN ⇒ MK=MN. Доказали, значит MNLK это параллелограмм у которого все стороны равны, то есть это ромб.
Обозначим вершины восьмиугольника АВСDЕFGH и проведём из вершины А диагонали АС = АG, AD = AF и AE.
Из тр-ка АВС (АВ=ВС=1,6м и уг.В = 135°) найдём АС по теореме косинусов:
АС² = АВ² + ВС² - 2·АВ·ВС·cos 135°
АС² = 1.6² + 1.6² - 2·1.6·1.6·cos 135°= 2.56 + 2.56 + 2.56·√2 =
= 2.56(2 +√2)
AC = 1.6·√(2 +√2)
Диагональ АЕ = СG, а СG можно найти из тр-ка АСG (AC = AG =1.6·√(2 +√2), и уг. CAG = 135°- 45° = 90°)
CG² = 2АС² = 2·2.56·(2 +√2) = 2.56·(4 +2√2)
CG = AE = 1.6·√(4 +2√2)
Диагональ АD находим из тр-ка АДЕ (АЕ = 3.2·√(1 +0.5√2), DE = AB = 1.6б уг. АDE = 90°)
AD² = AE² - DE² = 4·2.56·(1 +0.5√2) - 2.56 = 4·2.561 + 2·2.56·√2) - 2.56 =
= 2.56·(3 +2√2).
AD = 1.6·√(3 +2√2)