1) ∡МНО = 45
2) 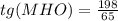
Объяснение:
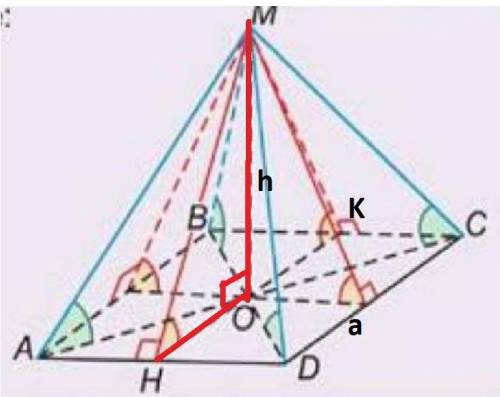
Рассчитайте величину двугранного угла при основании правильной четырехугольной пирамиды если:
1.сторона основания равна 3,6 м, а высота равна 1,8 м
(ABCD-квадрат) а = 3,6
ΔMOH OH = 0.5a=1.8; OM ⊥ OH; MO= 1,8 ⇒ ΔMOH прямоугольный равнобедренный ОМ = ОН = 1,8; ∡МОН = 90° ⇒ ∡МНО = 45
2.сторона основания равна 65 см, а высота равна 99 см
(ABCD-квадрат) а = 65
ΔMOH OH = 0.5a=65/2 OM ⊥ OH; MO= 99 ⇒ ΔMOH прямоугольный ∡МОН = 90° ⇒ 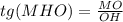
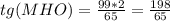
известен тангенс угла, а следовательно и сам угол при необходимости можно найти по таблицам Брадиса
1239,18 см², 3246,62 см².
Объяснение:
Вопрос 1:
Для начала найдём площадь всей фигуры с незакрашенным участком.
Ширина(b) прямоугольника = 32 см.
S=ab.
32×40=1280 см².
Затем найдём площадь всего незакрашенного участка.
S=пR².
4п - площадь меньшего круга. (12,56 см²).
9п - площадь большего круга. (28,26 см²).
12,56+28,26=40,82 см².
1280-40,82=1239,18 см². - S закрашенной фигуры.
Вопрос 2:
a прямоугольника = 60 см.
S прямоугольника = 55×60= 3300 см².
S меньшего круга =3,14 см². Это могло произойти только при том условии, что его R = 1 см.
16×3,14=50,24 см². - S большего круга.
3300-(3,14+50,24)=3246,62 см². - S закрашенной фигуры.
2. 10, 5 и 18,5 см
3. 35
4. 140