Объяснение: ЗАДАНИЕ 1
Проведём из вершины В высоту ВН. Так как треугольник равнобедренный то высота проведённая к основанию является ещё медианой и делит основание АС пополам, поэтому АН=НС=10÷2=5см.
Рассмотрим полученный ∆АВН. Он прямоугольный, а АН и ВН являются катетами, а АВ гипотенузой. По теореме Пифагора найдём катет ВН
ВН²=АВ²-АН²=13²-5²=159-25=144;
ВН=√144=12см.
И сейчас мы можем найти синус, сосинус и тангенс угла АВН:
Синус- это отношение противолежащего от угла катета к гипотенузе, поэтому sinABH=5/13
Косинус -это отношение прилежащего к углу катета к гипотенузе , поэтому
cosABH=12/13
Тангенс - это отношение противолежащего от угла катета к прилежащему. Поэтому:
tgABH=5/12
ответ: sinABH=5/13; cosABH=12/13;
tgABH=5/13
ЗАДАНИЕ 3
sinA=5/8
cosA=3/8
tgB=3/5
ЗАДАНИЕ 5
Найдём АВ через синус угла:
АВ=6÷sin24°; (sin24°≈0,4067)
AB=6÷0,4067≈14,75
Мы нашли гипотенузу АВ и теперь найдём по теореме Пифагора АД:
АД²=АВ²-ВД²=14,75²-6²=
=217,56-36=181,56; АД=√181,56≈13,47
Так как АД=ДС, то
АС=13,47×2=26,94см
ответ: АС=26,94см; АВ=ВС=14,75см


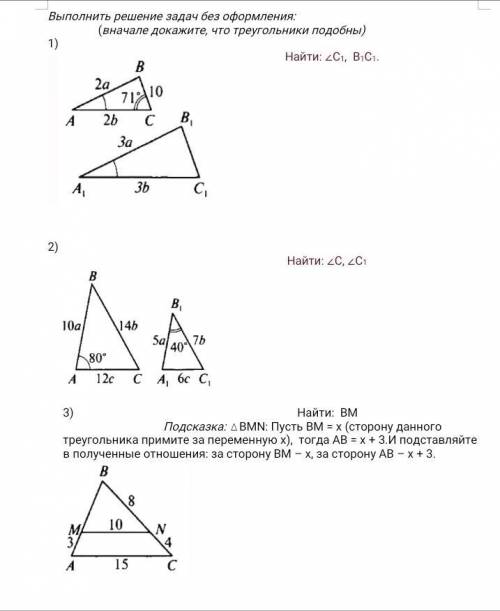
1) данные треугольники подобны, т.к углы ВАС и В1А1С1 равны, а стороны АВ и АС первого треугольника пропорциональны сторонам А1В1 и А1С1 соответственно АВ/А1В1=АС/А1С1=2/3. (по 2 признаку подобия)
Тогда угол С1= углу С= 71°. ВС/В1С1=2/3. В1с1=ВС×3/2=10×3/2=15.
2)треугольники подобны по 3 признаку подобия: АВ:А1В1=АС:А1С1=ВС:В1С1=2/1 (т.к. 10а/5а=2, 14в/7в=2 и 12с/6с=2)
Угол С=180°-угол А-угол В. Угол В= углу В1=40°. Угол С=180-80-40=60°. Угол С1=углу С=40°.
(Соответсвенные углы подобных треугольников равны)
3) треугольники ABC и MBN подобны по 1 признаку угол В общий, угол ВМN= BAC- соответственные (это если АС и NM параллельны по условию мало данных) тогда BM:AB=BN:BC=MN:AC. Возьмем ВМ за х. Тогда АВ - х+3. ВС=8+4=12. BM:AB=MN:AC. x:(x+3):10:15. x:(x+3)=2/3. 2×(x+3)=3x. 2x+6=3x. -x=-6, x=6.
BM=6