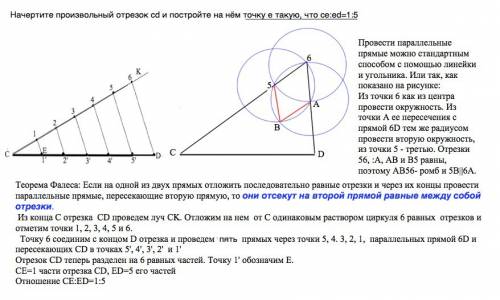
Теорема Фалеса: Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Из конца C отрезка CD проведем луч CK. Отложим на нем от С одинаковым раствором циркуля 6 равных отрезков и отметим точки 1, 2, 3, 4, 5 и 6.
Точку 6 соединим с концом D отрезка и проведем пять прямых через точки 5, 4. 3, 2, 1, параллельных прямой 6D и пересекающих CD в точках 5', 4', 3', 2' и 1'
Отрезок CD теперь разделен на 6 равных частей.
Точку 1' обозначим Е.
СЕ=1 часть отрезка СD, ED=5 его частей
Отношение CE:ED=1:5
подобны и треугольники ВОС и AOD, и CO/OA = BC/AD = 1/4; то есть AO = 4*CO; AC = AO + OC = 4*OC + OC = 5*AC; CO = AC/5;
отсюда MO = CM - CO = AC*(1/3 - 1/5) = AC*2/15;
Точно так же показывается, что NO = BD*2/15; (ясно, что BO = DO/4; откуда BD = BО +OD = BO + 4*BO = 5*BO; а из подобия треугольников BNC и PMD => BN/ND = BC/PD = 1/2; ND = 2*BN; BD = ND + BN = 3*BN; далее ON = BN - BO = BD*(1/3 - 1/5) = BD*2/15);
Если провести CК II BD, точка К лежит на продолжении AD, то BDKC – параллелограмм, и CK = BD; и угол AOD = угол ACK;
треугольник ACK подобен треугольнику MON, потому что соответственные стороны пропорциональны (NO = BD*2/15 = CK*2/15; MO = AC*2/15, угол AOD = угол ACK). Коэффициент подобия равен 2/15.
Поскольку AK = AD + BC, площадь треугольника ACK равна H*(AD + BC)/2, где H – расстояние от С до AD, то есть – высота трапеции.
То есть площадь ACK равна площади трапеции S.
Отсюда площадь MON равна S*(2/15)^2 = 50*4/225 = 8/9;