Объяснение:
1
a)М-середина
х=(5-3)/2=1 y=(-2+4)/2=1 z=(1+7)/2=4
M(1;1;4)
b)5=(x-3)/2⇒x-3=10⇒x=13
-2=(y+4)/2⇒y+4=-4⇒y=-8
1=(z+7)/2⇒z+7=2⇒z=-5
C(13;-8;-5)
2
a+b={1;-4;1}
|a+b|=√1+16+1=√18=3√2
|a|+|b|=√4+36+9+√1+4+4=√49+√9=7+3=10
3
AB=√(1-2)²+(-5-1)²+(0+8)²=√1+36+64=√101
BC=√(8-1)²+(1+5)²+(-4-0)²=√49+36+16=√101
AC=√(8-2)²+(1-1)²+(-4+8)²=√36+0+16=√52=2√13
AB=BC- треугольник равнобедренный
Средняя линия равна 1/2АС=1/2*2√13=√13
Пусть N(x;y;z)- произвольная точка плоскости.
Тогда векторы NM и n - ортогональны.
Условием ортогональности является равенство нулю их скалярного произведения.
Находим координаты векторов.
NM (2-x;3-y;5-z)
n(4;3;2)
Находим их скалярное произведение - это сумма произведений одноименных координат
4(2-х)+3(3-у)+2(5-z)
и приравниваем к нулю
4(2-х)+3(3-у)+2(5-z) =0
или
8-4х+9-3у+10-2z=0
4x+3y+2z-27=0
ответ. 4х+3у+2z-27=0
Подробнее - на -
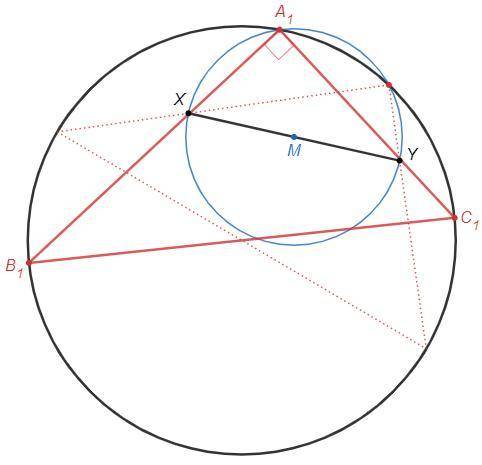
Дана окружность и точки X и Y внутри нее.
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.
<DCF = < DCE : 2 = 80/2 = 40 гр. ( CF - биссектриса)
< CFD = 180 - <D - <DCF = 180 - 68 - 40 = 72 гр.( сумма углов треугольник ровна 180 градусов)
ответ: 72 гр.