1. Теорема пифагора
3²+4²=х²
Вычислить
25=х²
х=5
2. 13 гипотенуза
4²+х²=13²
Отнять от обоих сторон 4²
х²=13²-4²
Использовать а²-б²=(а+б)(а-б)
х²=17*9
Квадратный корень от обоих сторон
х = 3√17
3. Это прямоугольный треугольник с равными катетами. Значит гипотенуза это 2√5² (корень и квадрат удалятся)
2×5=х²
Корень обоих сторон
х=√10
4. х - прилежащая сторона
cos(30°) = прилеж./гипотенуза
cos(30°) = х/2√3
Найдите значение cos(30°) на калькуляторе или таблице
(√3)/2 = х/2√3
Умножить стороны на 2√3, √3 * √3 будет 3
2*3/2 = х
Перекреслить 2
х = 3
5. Низ треугольника 16
Треугольник состоит из двух прямоугольных треугольников, в которых нижний катет половина нижнего катета этого треугольника (8)
по теореме пифагора получается
8²+х²=17²
Отнять 8² от обоих сторон
х²= 17²-8²
Вычислите: 17²=289, 8²=64, 289-64=225
Корень обоих сторон
х = 15
6. Так как треугольник правильный (равносторонний) все стороны как правило 6, снова будет 2 прямоуг. Треугольника получаться .. (довольно аналогично предыдущей задаче)
3²+х²=6²
х²=36-9
х=√27
запишите 27 как 3²*3
х= √(3²*3)
Извлечь корень обоих множителей
х= √3²*√3
х = 3√3
7. Похоже на предыдущую задачу.
х²-8²=(х/2)²
Возвести дробь в степень, возвев в эту степень знаменатель и числитель, прибавить 64 к обоим сторонам
х²=х²/4+64
умножить на 4 обои стороны
4х²=х²+256
перенести х² влево и сменить знак.
4х²-х²-256 = 0
3х²=256
Делить на 3 стороны
х²=256/3
Корень обоих сторон, использовать свойство корней снова
х= (√256)/√3
8. 10²+х²=26²
Перенести 10 вправо и сменить знак
х²=26²-10²
Используйте а²-б²= (а+б)(а-б)
х²=(26+10)(26-10)
х²=36*16
Записать как 6² и 4², умножить степени одинаковых показателей умножив основания.
х²=(6*4)²
Корень обоих сторон
х=24
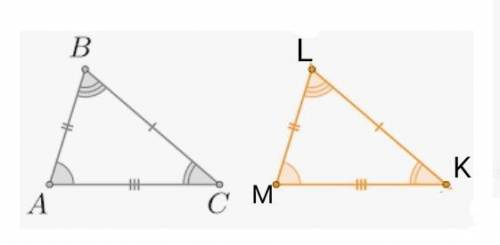
Объяснение:
1) фото чертежа прилагаю...
∆ABC=∆MKL
AB=ML
<B=<L
BC=LK
AC=MK
<A=<M
<C=<K
2)
Пусть одна сторона будет х, тогда вторая сторона будет 4х, а третья сторона будет (х-14).
Составляем уравнение
х+4х+х-14=166
6х=166+14
6х=180
х=180/6
х=30 см первая сторона
4*30=120 см вторая сторона
30-14=16 см третья сторона.
ответ: 30см; 120см; 16см
3)
1дм=10см
12дм=120см
1)3+7+5=15 коэффициент
2) 120:15=8 одна часть коэффициента.
3) 8*3=24 см первая сторона треугольника
4) 7*8=56 см вторая сторона треугольника.
5) 5*8=40 см третья сторона треугольника
ответ: 24см; 56см;40см.
Решение задачи с уравнения.
Пусть одна сторона будет 3х см, вторая сторона 7х см; третья 5х см.
Составляем уравнение.
3х+7х+5х=120
15х=120
х=120/15
х=8
8*3=24 см первая сторона
7*8=56 см вторая сторона
5*8=40 см третья сторона.
ответ: 24см; 56см;40см.
Более того, одно из возможных решений сразу видно - середина отрезка AQ удалена от точек A и Q на 2, и от стороны BC тоже, то есть 2 - одно из возможных решений. К сожалению - не единственное.
Центр окружности удален от стороны BC на r - величину радиуса. Расстояние от центра до стороны AC я обозначу q; для окружности (оси X и Y - это просто стороны BC и AC)
(x - q)^2 + (y - r)^2 = r^2; (такая окружность заведомо касается прямой ВС - есть только одна общая точка (q, 0), остальные точки лежат заведомо выше ВС)
известно, что она проходит через точку А (0,3) и Q(2√3,1) откуда получаются два уравнения
q^2 + 9 - 6r = 0;
(2√3 - q)^2 + 1 - 2r = 0; или q^2 - 4√3q + 13 - 2r = 0;
если вычесть одно из другого, получится q = (r + 1)/√3; и подстановка этого в первое дает
r^2 - 16r + 28 = 0; или (r - 2)(r - 14) = 0;
то есть кроме ответа r = 2; возможно решение r = 14;
Конечно, когда это известно, и понятно, где находится центр второго решения
- для второго решения q = 5√3; а ВС = 3√3, точка касания как раз находится на прямой ВС на расстоянии q = 5√3 от С, - можно получить ту же самую систему уравнений для r и q, не используя уравнение окружности, а просто сравнивая расстояния от возможного центра до точек A Q и прямой BC. Получится то же самое уравнение на r.
Например, можно записать свойство касательной и секущей из точки B
(q - 3√3)^2 = 2*6; q = 3√3 +- 2√3; и получилось оба решения :) после нахождения q остается найти r. Такое решение кажется технически проще, но это не так - чтобы найти r, зная q, надо постараться, даже зная ответ :).