14√2+12
Объяснение:
Так как боковая грань пересекается с меньшей стороной при основании с 45 градусов, то высота будет равна половине второй стороне при основании, из-за того что проекция образует равнобедренный прямоугольный треугольник.
Площадь боковой поверхности пирамиды определяется нижеуказанной формулой:
S=Ph/2
где, P периметр основания, h высота (апофема).
P=2(3+4)=14
h=2√2
S=14*2√2/2=14√2
Площадь основания пирамиды:
S=a*b=4*3=12
Площадь полной поверхности пирамиды:
S(пол)=S(бок)+S(осн)=14√2+12
ответ: 14√2+12
О (0;9).
Объяснение:
1. Точка, лежащая на оси ординат, имеет абсциссу, равную нулю. Обозначим искомую точку О (0;у).
По условию О равноудалена от А(3;2) и В(7;6), тогда
ОА = ОВ.
ОА^2 = (3-0)^2 + (2-у)^2 = 9 + (2-у)^2.
ОВ^2 = (7-0)^2 + (6-у)^2 = 49 + (6-у)^2.
Составим и решим уравнение:
9 + (2-у)^2 = 49 + (6-у)^2
9 + 4 - 4у + у^2 = 49 + 36 -12у + у^2
13 - 4у = 85 -12у
12у - 4у = 85 - 13
8у = 72
у = 72 : 8
у = 9
О (0;9) - искомая точка.
Проверим полученный результат:
О (0;9), А(3;2) и В(7;6)
ОА^2 = (3-0)^2+(2-9)^2 = 9+49 = 58;
ОВ^2 = (7-0)^2+(6-9)^2 = 49+9 = 58.
ОА = ОВ - верно.
Длина перпендикуляра, проведённого из данной точки к данной прямой, называется расстоянием от этой точки к этой прямой.
#1.
Этим расстоянием будет являться отрезок BM, его длину нужно найти. Этот отрезок представляет собой катет прямоугольного треугольника, лежащий напротив угла в 30°. По свойству прямоугольного треугольника такой катет будет равен половине гипотенузы, в данном случае – AM. AM = 26, следовательно BM = 13.
ответ: 13.
#2. Сумма острых углов прямоугольного треугольника по его свойству должна быть равна 90°, тогда угол M + угол A = 90°, а так как угол M = 60°, то угол A = 30°. Нам требуется найти BM. BM – это катет, лежащий напротив угла в 30°, значит BM = 1/2 × AM, а так как AM = 30, то BM = 15.
ответ: 15.
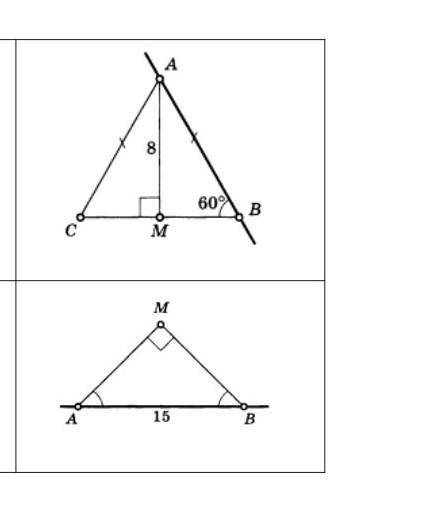
#5. Я прикрепил рисунок к заданию. Нам нужно будет найти расстояние от точки M до AB, то есть перпендикуляр MF. Сумма острых углов прямоугольного треугольника равна 90°, тогда угол B + угол A = 90°. Угол B = 60° по условию, значит угол A = 30°. Тогда MF = 1/2 AM, так как MF – катет, лежащий напротив угла в 30. AM по условию равно 8, значит MF = 4.
ответ: 4.
#6. Рисунок к заданию прикрепил. Так как требуется найти расстояние от точки M до отрезка AB, то нужно найти перпендикуляр ME. Это задание можно решить двумя :
#1. ME – перпендикуляр, проведённый из вершины треугольника ABM, значит ME – высота. В треугольнике AMB два угла равны, значит треугольник равнобедренный. А в равнобедренном треугольнике высота, проведённая к основанию, является медианой, то есть ME – медиана. Есть свойство прямоугольного треугольника, которое гласит, что медиана, проведённая из вершины прямого угла прямоугольного треугольника, равна половине гипотенузы, тогда ME = 1/2 × AB, а раз AB = 15 по условию, то ME = 7,5.
#2. В прямоугольном треугольнике сумма острых углов равна 90°, то есть угол A + угол B = 90°, а раз они равны, то угол A = углу B = 45°, тогда треугольник AMB – равнобедренный. ME – перпендикуляр, а значит треугольники AME и BME – прямоугольные. В прямоугольном треугольнике сумма острых углов равна 90°, то есть угол BME + угол B = 90° и угол A + угол AME = 90°. Углы A и B = 45°, как мы уже убедились, значит углы BME и AME = 45°. Тогда треугольники AME и BME – равнобедренные, а значит в этих треугольниках боковые стороны равны. Тогда ME = AE и ME = BE. Треугольник AMB – равнобедренный, ME – высота, а значит ME – медиана, тогда AE = BE. Эти стороны образуют AB, которая равна 15, значит AE = BE = 7,5. А так как ME равна этим сторонам, то ME = 7,5.
ответ: 7,5.
Объяснение: