Дано: (рисунок)
Найти: AB
Решение: Опустим на сторону BC вершину AD, проходящую через точку A.
Так как вершина является перпендекуляром, то углы ADC и ADB равны 90⁰.
Так как сумма углов треугольника равна 180⁰, найдем углы CAD и DAB:
угол CAD=180⁰-30⁰-90⁰=60⁰
угол DAB=180⁰-90⁰-45⁰=45⁰
Из последнего выражения следует, что треугольник ADB - равнобедренный.
Найдем сторону AD треугольника CAD, пользуясь выражением «в прямоугольном треугольнике катед против 30⁰ равен половине гипотенузы»:
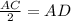
AD=6 см
Так как треугольник ADB равнобеднеррый, то AD=DB
Теперь, найдем сторону AB по теореме Пифагора:
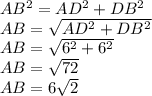

Найдите углы A и B треугольника ABC, если AB=12 см, BC=6√6 см, угол C= 45°.
ответ: 60° , 75° или 120° , 15° .
Объяснение:
По теореме синусов : BC / sin(∠A) =AB / sin(∠C ) ⇔
6√6/sin(∠A)=12/sin45°⇔sin(∠A) =6√6*sin45°/12=6√6 *(√2/2) / 12 = 3 /2 ⇒
∠A= 60° или ∠A= 120° . Оба верны ∠A > ∠C , т.к. BC > AB
( в треугольнике против большой стороны лежит большой угол )
* * * BC > AB : BC = 6√6 > 6√4 = 12 = AB * * *
∠B = 180° - (∠A+√C) → ∠B = 75° или ∠B = 15° см. лишнее приложение