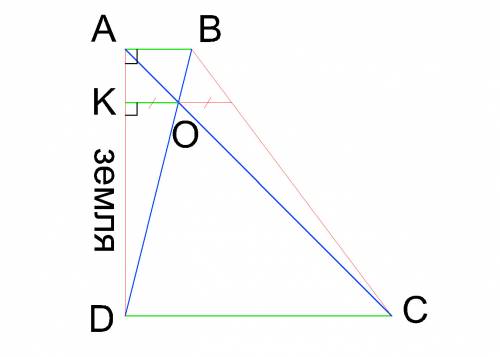
Шесты АВ и ДС как основания образуют прямоугольную трапецию АВСД, а пересечение канатов ВД и СА есть не что иное, как пересечение диагоналей прямоугольной трапеции.
Как известно, отрезок, параллельный основаниям и проходящий через пересечение диагоналей прямоугольной трапеции делится точкой пересечения пополам, и если АВ=х, ДС=у, то длина его равна 2·х·у/(х + у).
Исходя из этого: ОК=2·х·у/(х + у)÷2=х·у/(х + у)
1) ОК=(х·у)÷(х + у)
Как видно, длина ОК никаким образом не зависит от расстояний между шестами, а лишь от их высоты.
2) Если AB=х=2 м, а DC=у=8 м, то ОК=(2·8)÷(2+8)=1,6 м
ответ: длина шеста ОК=1,6 м
Проще всего решить эту задачу "с конца". В какой-то точке пространства проведем три взаимно перпендикулярные прямые, то есть координатные оси. На этих осях выберем точки с координатами A(1,0,0) B(-1,0,0) C(0,1,0) D(0,0,1). Легко видеть, что AC = CD = DA = CB = DB; поэтому треугольники ACD и BCD равносторонние, и углы между СD и CA, а также CD и CB равны 60 градусов. Так же очевидно, угол ВСА = 90 градусов. То есть трехгранный угол С как раз такой, какой задан в задаче.
Осталось заметить, что CD составляет угол 45 градусов с плоскостью XY (то есть плоскостью АВС). В самом деле, СОD - прямоугольный равнобедренный треугольник, что и требовалось доказать.
А есть еще такое "веселое" решение (смотри чертеж). Возьмем обычный куб, выберем любую вершину (ну, В, например), и проведем сечение через концы ребер, выходящих из этой вершины (через А С и В1). Такое сечение - равносторонний треугольник АСВ1 (АС = СВ1 = АВ1), то есть угол АСВ1 = 60 градусов. Получилась пирамида АВ1СВ. Я возьму еще одну точно такую же пирамиду (на чертеже МСВВ1), и приставлю к этой так, чтобы получился нужный трехграный угол (на чертеже это угол, образованный лучами AC, B1C и MC - ясно, что угол АСМ = 90 градусов). При таком подходе вопрос в задаче - это даже не вопрос, а так, сотрясение воздуха :))) Угол В1СВ по построению 45 градусов.