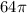см³.
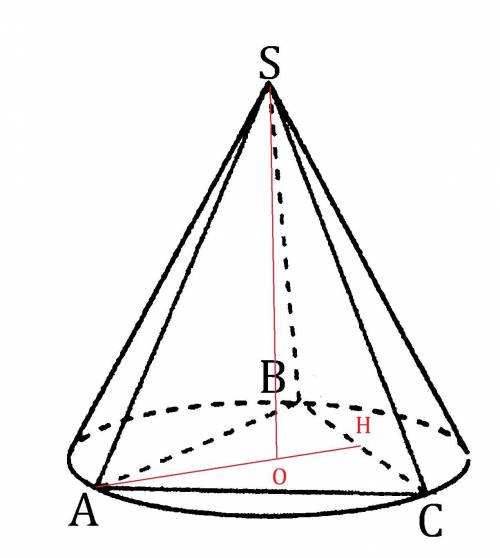
Обозначим данную пирамиду буквами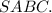 
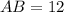см.
Проведём высоту пирамиды SO.
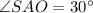
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
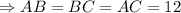см.
Проведём высоту 
в 
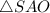- прямоугольный, так как 
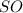- высота пирамиды.
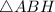- прямоугольный, так как - высота .
Так как - равносторонний ⇒ - высота, медиана и биссектриса
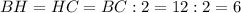см, так как - медиана.
Найдём по теореме Пифагора 
.
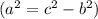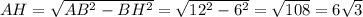см.
Точка 
- пересечение медиан и делит их в отношении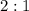 
, считая от вершины.
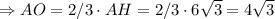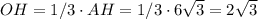см
см.
Также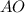 
- радиус описанной около окружности.
Рассмотрим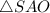
Если угол в прямоугольном треугольнике равен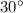 
, то напротив лежащий катет равен половине гипотенузы.
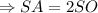
Составим уравнение:
Пусть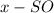 
, тогда 
.
И по теореме Пифагора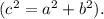 
конуса = 
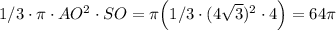см³.
Проведем перпендикуляр SO к плоскости основания и перпендикуляры SK, SM и SN к сторонам ΔABC. Тогда по теореме о трех перпендикулярах OK ⊥ BC, ОМ ⊥ АС и ON ⊥ AB.
Тогда, ∠SKO = ∠SMO = ∠SNO = 45° — как линейные углы данных двугранных углов.
А следовательно, прямоугольные треугольники SKO, SMO и SNO равны по катету и острому углу.
Так что OK=OM=ON, то есть точка О является центром окружности, вписанной в ΔАВС.
Выразим площадь прямоугольника АВС:
С другой стороны можно S=p×r
Так как в прямоугольном треугольнике SOK острый угол равен 45°, то ΔSOK является равнобедренным и SO=OK=3 см.
ответ: 3 см.