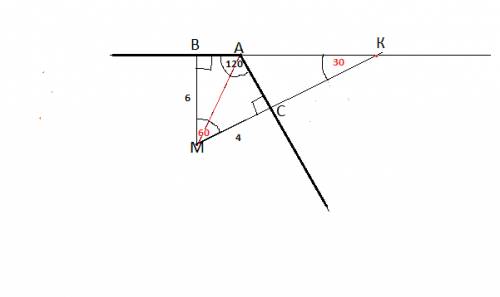
Точка М лежит внутри двугранного угла величиной 120 градусов и удалена от его граней на расстояния соответственно 4 и 6. Найдите расстояние от М до ребра двугранного угла.
Опишу подробно.
Рисуем данный угол 120° как бы в разрезе, т.е. вид сверху.
Обозначим вершину данного угла А.
В нутри угла отмечаем точку М.
Расстояние от точки до плоскости - перпендикуляр.
Опустим из М перпендикуляры к сторонам угла.
Обозначим точку пересечения со стороной угла более длинного отрезка, равного 6, - В , более короткого, равного 4, - С.
Т.к. сумма углов четырехугольника 360°, углы В и С прямые по построению, то
угол ВМС=180°-120°=60°.
Продлим сторону ВА и построим смежный с углом А угол.
Он, как смежный, равен 180°-120°=60°
Продлим МС до пересечения с ВА, обозначим точку пересечения К.
Получился прямоугольный треугольник ВМК.
В нем
угол ВМК равен 60° . угол ВКМ=30°
МК=ВМ:sin( 30°)=12
СК=МК-МС=12-4=8
АС=CК:Ctg (30°)=8:√3
Из прямоугольного треугольника АМС по теореме Пифагора найдем МА.
МА²=АС²+МС²=(8:√3)²+4²=64/3+16=112/3
МА=√(112/3)=4√(7/3)
14.722431864335(14.7)
Объяснение:Проведём биссектрису от угла у основания. Тк. треугольник равнобедренный,биссектриса поделила противоположную сторону пополам. 34:2=17(дм).Сумма всех углов треугольника равна 180 °. 180-60=120°(Два угла у основания).Так как треугольник равнобедренный, углы у основания равные.120:2=60°(угол).Исходя из этого можно понять, что треугольник,получившийвся в процессе проведения биссектрисы равносторонний.По формуле нахождения :
h=√3:2(←Это надо писать через черту дроби)*a
h=√3:2*17=14,722431864335
Можно округлить до десятых:
14.722431864335≈14.7
ответ:14.7 дм
Ндеюсь,что
V = Sосн*h = a²h
S = 2Sосн+Sбок = 2а²+4аh
Диагональ квадрата d = a√2, отсюда а=d/√2 = 5√2 cм
V = a²h = (5√2)²*12 = 600 см³
S = 2а²+4аh = 2*(5√2)² + 4*12*5√2 = 100+240√2 см²