Сторона ромба равна его диоганали найдите больший угол ромба

👇

Ответ:

tinakristina1234

25.09.2021

Т к сторона ромба равна его диагонали, то имеем равносторонний треугольник, углы которого по 60 градусов, и значит больший угол в ромбе составляет 60*2=120 градусов, т к диагональ является биссектрисой большего угла.
ответ 120 градусов

4,4(37 оценок)

Открыть все ответы

Ответ:

Maria2009

25.09.2021

1) Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.

То есть, если точка А лежит на единичной окружности, то её координаты можно записать так: $A(\, cosa\, ;\, sina\, )$ .

Основное тригонометрическое тождество имеет вид: 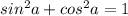sin^2a+cos^2a=1 .

Поэтому проверяем это тождество для заданных координат.

$A\Big(\, \dfrac{1}{2}\, ;-\dfrac{1}{2}\, \Big):\ \ \Big(\dfrac{1}{2}\Big)^2+\Big(-\dfrac{1}{2}\Big)^2=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\ne 1\\\\\\B\Big(\dfrac{\sqrt3}{2}\, ;-\dfrac{1}{2}\, \Big):\ \ \Big(\dfrac{\sqrt3}{2}\Big)^2+\Big(-\dfrac{1}{2}\Big)^2=\dfrac{3}{4}+\dfrac{1}{4}=1\ \ \to \ \ B\in okryznosti\\\\\\C\Big(-\dfrac{\sqrt3}{4}\, ;\, \dfrac{1}{4}\, \Big):\ \ \Big(-\dfrac{\sqrt3}{4}\Big)^2+\Big(\dfrac{1}{4}\Big)^2=\dfrac{3}{16}+\dfrac{1}{16}=\dfrac{1}{4}\ne 1$

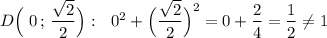
$D\Big(\; 0\, ;\, \dfrac{\sqrt2}{2}\Big):\ \ 0^2+\Big(\dfrac{\sqrt2}{2}\Big)^2=0+\dfrac{2}{4}=\dfrac{1}{2}\ne 1$

На единичной окружности лежит точка 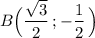$B\Big(\dfrac{\sqrt3}{2}\, ;-\dfrac{1}{2}\, \Big)$ .

Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.

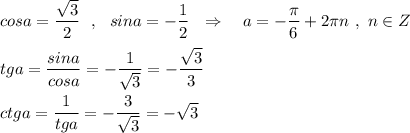
$cosa=\dfrac{\sqrt3}{2}\ \ ,\ \ sina=-\dfrac{1}{2}\ \ \Rightarrow \ \ \ a=-\dfrac{\pi}{6}+2\pi n\ ,\ n\in Z\\\\tga=\dfrac{sina}{cosa}=-\dfrac{1}{\sqrt3}=-\dfrac{\sqrt3}{3} \\\\ctga=\dfrac{1}{tga}=-\dfrac{3}{\sqrt3}=-\sqrt3$

Смотри рисунок.

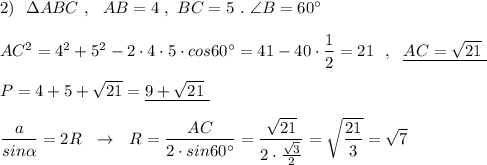
$2)\ \ \Delta ABC\ ,\ \ AB=4\ ,\ BC=5\ .\ \angle B=60^\circ \\\\AC^2=4^2+5^2-2\cdot 4\cdot 5\cdot cos60^\circ =41-40\cdot \dfrac{1}{2}=21\ \ ,\ \ \underline {AC=\sqrt{21}\ }\\\\P=4+5+\sqrt{21}=\underline {9+\sqrt{21}\ }\\\\\dfrac{a}{sin\alpha }=2R\ \ \to \ \ R=\dfrac{AC}{2\cdot sin60^\circ }=\dfrac{\sqrt{21}}{2\cdot \frac{\sqrt3}{2}}=\sqrt{\dfrac{21}{3} }=\sqrt7$

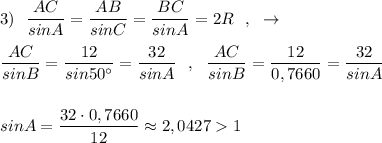
$3)\ \ \dfrac{AC}{sinA}=\dfrac{AB}{sinC}=\dfrac{BC}{sinA}=2R\ \ ,\ \ \to \\\\\dfrac{AC}{sinB}=\dfrac{12}{sin50^\circ }=\dfrac{32}{sinA}\ \ ,\ \ \dfrac{AC}{sinB}=\dfrac{12}{0,7660}=\dfrac{32}{sinA}\\\\\\sinA=\dfrac{32\cdot 0,7660}{12}\approx 2,04271$

Так как sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .

4,6(36 оценок)

Ответ: