Из Δ АНС: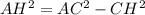
Из Δ АНВ: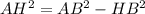
Пусть СН=х,тогда НВ=20-х
Приравняем:
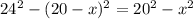

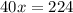
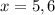
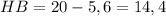
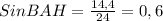
параллелограмм АВСД, АВ=СД, АД=ВС, проводим высоту ВК на СД, площадь АВСД=СД*ВК, М - произвольная точка (для построения - если считать точку О пересечение диагоналей то М по диагонали АС между А и О , ближе к О), через точку М проводим линию параллельную ВК, на АВ она пересекается в точке К, на продолжении СД в точке Т,
КМ-высота для треугольника АВМ, площадь треугольника АВМ=1/2*АВ(СД)*МК,
МТ-высота для треугольника СМД, площадь СМД=1/2*СД(АВ)*МТ, площадь АВМ+площадьСМД=1/2*СД*МК+1/2*СД*МТ=1/2СД*(МК+МТ), но МК+МТ=КТ, а КТ=ВК, тогда площадь АВМ+площадь СМД=1/2*СД*ВК, т.е=1/2 площади АВСД
Ну, начнем с того, что проведем высоту СК к стороне АВ и рассмотрим треугольник ВСК.
Опять (3,4,5) :)))
Ясно, что треугольник ВСК имеет катет ВК = АВ/2 = 12 и гипотенузу ВС = 20, то есть это треугольник (3,4,5), увеличенный в 4 раза.
(Само собой, СК = 16; это не пригодится.)
Поэтому косинус угла СВК равен 3/5.
Я даже не буду дальше что-то объяснять -
угол ВАН = 90 - угол СВК;
поэтому, как говорят шахматисты, мат на доске.
ответ синус угла ВАН = 3/5.